Fisher's exact test is a non parametric statistical method used to compare the differences in the distribution of two categorical variables. It is suitable for small samples or discrete data, and does not require the assumption of a normal distribution.

    Fisher's exact test is a non parametric statistical test method proposed by statistician Ronald Fisher, used to compare the correlation between two categorical variables. It is particularly suitable for small sample data or data with certain special conditions. This test can help us determine whether there is a significant correlation between two variables, without relying on the distribution assumption of the data.

    In this Fisher exact test result, we analyzed two factors: whether it is an only child and gender.

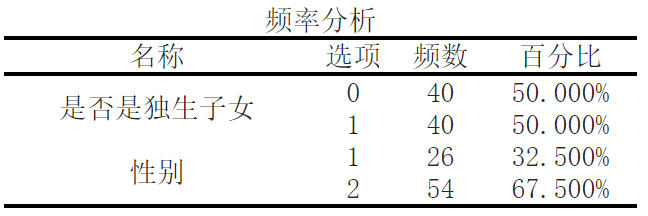
     According to frequency analysis, there are 40 out of 0.0 only children, accounting for 50.00%; Among the only children, there are 40 out of 1.0, accounting for 50.00%.

     There are 26 gender 1.0, accounting for 32.50%; There are 54 gender 2.0, accounting for 67.50%.

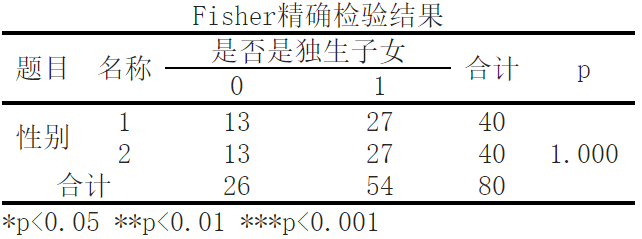
    If the P-value is greater than or equal to 0.05 and does not show significance, accepting the original hypothesis indicates that there is no significant difference between the categorical variable X and the categorical variable Y

    In this Fisher exact test result, we analyzed two factors: whether it is an only child and gender. Fisher's exact test is a statistical test method used to compare whether there is a significant correlation between two categorical variables.

    In this test result, we can see the correlation between gender and whether one is an only child. In this example, the p-value is 1.000, which is greater than the usual significance level of 0.05. Therefore, we cannot conclude that there is a significant correlation between the two factors.

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。