The homogeneity test of variance is used to test whether the variances between different samples or groups are equal. It is a commonly used test method in statistical analysis to determine whether the hypothesis of homogeneity of variance can be applied. The homogeneity test of variance is used to check whether the variances between two or more samples or populations are equal. Homogeneity of variance is one of the prerequisites for many statistical methods such as linear regression and analysis of variance. The commonly used methods for testing homogeneity of variance include Levene's test and Bartlett's test. If the variance is uneven, it may lead to incorrect interpretation and inference of the data.

    The homogeneity test of variance is used to check whether the data variances of different samples or groups are equal. When conducting some statistical analysis, such as analysis of variance (ANOVA), homogeneity of variance is an important assumption. If the assumption of homogeneity of variance is not met, other statistical methods may need to be used to analyze the data.

    Data description:

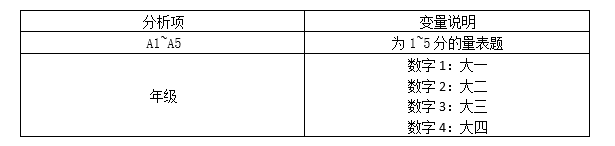
    Background description:

    These data provide F and p values for different grades to test whether the variance of the data for different grades is equal. There may be differences in certain variables (such as grades) between different grades. Based on the given p-value, we can infer that there is no statistically significant difference in data variance between these grades. This means that the data variances between these grades are similar, meeting the assumption of homogeneity of variances, and statistical methods such as analysis of variance can continue to be used to analyze the data.

    The results show:

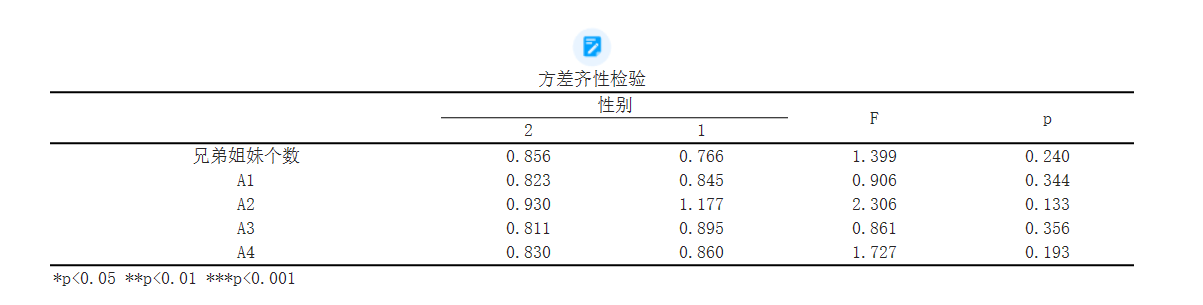
    The results of the homogeneity of variance test show that for A1, its F-value is 0.835, and the significance P-value is 0.479>0.05. It does not show significance at the level, and the original hypothesis cannot be rejected. Therefore, the data meets the homogeneity of variance, and analysis of variance can be used.

    The results of the homogeneity of variance test show that for A2, the F-value is 1.617, and the significance P-value is 0.192>0.05. There is no significant difference at the level, and the original hypothesis cannot be rejected. Therefore, the data meets the homogeneity of variance, and analysis of variance can be used.

    The results of the homogeneity of variance test show that for A3, the F-value is 1.945, and the significance P-value is 0.129>0.05. There is no significant difference at the level, and the original hypothesis cannot be rejected. Therefore, the data meets the homogeneity of variance and analysis of variance can be used.

    The results of the homogeneity of variance test show that for A4, the F-value is 0.482, and the significance P-value is 0.696>0.05. There is no significant difference at the level, and the original hypothesis cannot be rejected. Therefore, the data meets the homogeneity of variance, and analysis of variance can be used.

    The results of the homogeneity of variance test show that for A5, the F-value is 2.298, and the significance P-value is 0.084>0.05. There is no significant difference at the level, and the original hypothesis cannot be rejected. Therefore, the data meets the homogeneity of variance, and analysis of variance can be used.

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。