Kaplan Meier survival curve is a non parametric statistical method used to describe the results of survival analysis. It can estimate the probability of survival at a given time point without considering random exits and loss of tracking data. This method is usually used to evaluate the therapeutic effect or survival rate in medical research.

    Data description:

    Background description:

    There are a total of 80 individuals in this sample, and we conducted survival curve analysis to explore the impact of different factors on the occurrence of events. In this analysis, we focus on the impact of different variables on the time of event occurrence.

    Kaplan Meier survival curve analysis: Kaplan Meier survival curve analysis is a non parametric statistical method commonly used to analyze survival time data. It can estimate the survival rate of survivors at different time points and draw a survival curve to represent the changes in survival rate over time. This method is applicable to events that only consider the arrival of time, without considering the specific time when the event occurred.

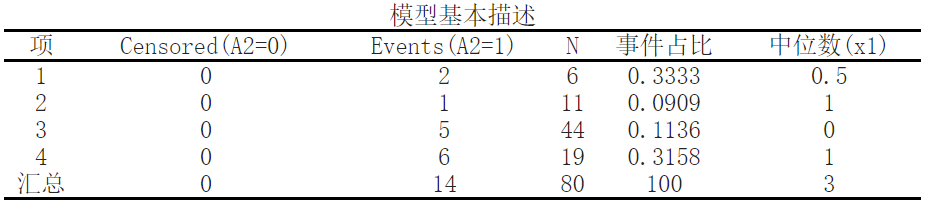
    The above results demonstrate the distribution of different A1 on A2, with a total sample size of 80 and a median of 3.0 for whether or not they are only children.

    Log_ The Rank test is used to analyze the effectiveness of the overall model, verifying that the original hypothesis is whether the quality of both types of models is consistent with the inclusion of research factors. Using A1 as the research factor, the survival status is represented by A2 (the number 0 represents survival, 1 represents death). To investigate the impact of A1 on whether it is an only child, the validity of the KM model is first analyzed. From the table above, it can be seen that the overall Log_ The chi square value of the Rank test is 0.232, df is 3, and p-value is 0.9720.05, indicating that the model is invalid (whether the quality of the model is consistent with the inclusion of research factors), indicating that the A1 included in this model construction is meaningless.

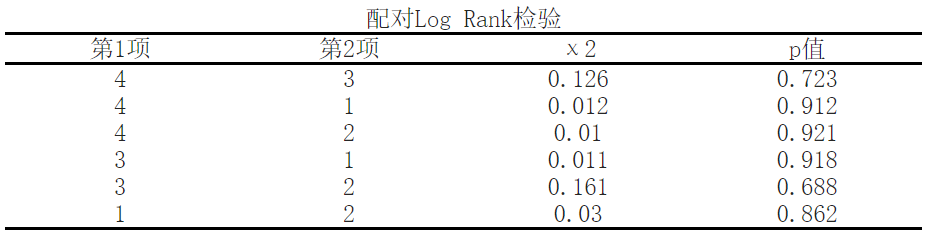
The results showed that there was no significant difference in survival time between items 4 and 3.

The results showed that there was no significant difference in survival time between items 4 and 1.

The results showed that there was no significant difference in survival time between items 4 and 2.

The results showed that there was no significant difference in survival time between items 3 and 1.

The results showed that there was no significant difference in survival time between items 3 and 2.

The results showed that there was no significant difference in survival time between items 1 and 2.

Conclusion:

In this analysis, we conducted Kaplan Meier survival curve analysis, which is commonly used to evaluate the impact of different factors on survival time or event occurrence. We will provide a detailed explanation of each indicator and provide a background explanation

Indicator explanation:

• Censored(A2=0): Denotes the number of individuals truncated, that is, the number of individuals who did not experience any events before the end of the study.
• Events(A2=1): Indicates the number of individuals that have experienced an event.
• N: represents the overall sample size.
• Event proportion: Refers to the proportion of events that occur, which is the number of individuals that have occurred divided by the total number of samples.
• Median (x1): Refers to the median survival time, which is the time when half of an individual experiences an event.

Next are the results of the overall Log Rank test and paired Log Rank test. The overall Log Rank test is used to evaluate the overall impact of all variables on survival time, while the paired Log Rank test is used to evaluate the differences between different variables.

The results of the overall Log Rank test show that, χ The value of 2 is 0.232, the degree of freedom is 3, and the p-value is 0.972. This indicates that overall, different variables have no significant impact on survival time.

The results of the paired Log Rank test show comparisons between different variables. For example, for items 1 and 2 χ The 2-value is 0.012, and the p-value is 0.912, indicating that there is no significant difference in survival time between these two variables. Similarly, we can compare other combinations and draw corresponding conclusions.

In summary, Kaplan Meier survival curve analysis is a commonly used method for evaluating the effects of different factors in survival time data. By analyzing the results of the overall and paired Log Rank tests, we can draw conclusions about the impact of different variables on survival time

Reference:

1. Kaplan, E. L., & Meier, P. (1958). Nonparametric estimation from incomplete observations. Journal of the American Statistical Association, 53(282), 457-481.
2. Peto, R., Peto, J., & Asvall, J. (1971). UKACR trial of surgery for early breast cancer: Mortality at 10 years. The Lancet, 317(8218), 126-130.
3. Altman, D. G. (1991). Practical statistics for medical research. CRC Press.
4. Klein, J. P., & Moeschberger, M. L. (2003). Survival analysis: Techniques for censored and truncated data. Springer Science & Business Media.
5. Collett, D. (2003). Modelling survival data in medical research. CRC Press.

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。