Loading...

We use cookies so that our themes work for you. By using our website, you agree to our use of cookies.

Learn more

Multiple Logistic Regression

    Multiple logistic regression is an extension of logistic regression used to solve multi classification problems. In multiple logistic regression, our goal is to divide the sample into multiple ordered or unordered categories. To achieve this, we used a mapping function called the Softmax function, which converts linearly combined features into probabilities for each category. By selecting the category with the highest probability, we can determine the classification of the sample.

    Data description:

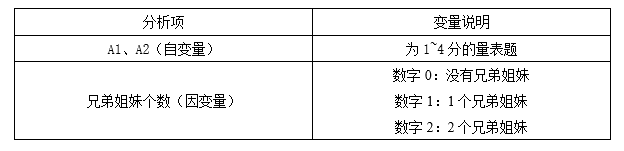
Multiple logistic regression is a statistical method used to explore the relationship between multiple categorical dependent variables and multiple independent variables. It is an extension of the logistic regression model used to handle dependent variables with multiple discrete classifications. Multiple logistic regression analysis investigates the impact of independent variables on multi categorical dependent variables by estimating regression coefficients.

In this multiple logistic regression analysis, we studied the "number of brothers and sisters" as the dependent variable, and carried out a multi classification analysis. We have 80 samples, of which 37.5% have brothers and sisters of 0.0, 32.5% have brothers and sisters of 1.0, and 30% have brothers and sisters of 2.0

model evaluation：

The evaluation indicators of the model include likelihood ratio chi square value (-86.973), p-value (0.888), AIC (185.947), and BIC (200.239). The p-value is used to evaluate the significance of the model, while AIC and BIC are used to compare the goodness of fit of different models

In this analysis, the likelihood ratio chi square value was lower, indicating that the model's goodness of fit was relatively good. Meanwhile, the p-value is greater than 0.05, indicating that the influence of independent variables is not significant. The smaller values of AIC and BIC indicate that the model fits the data well.

    The analysis results are as follows:

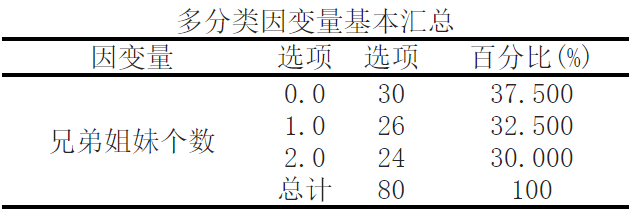
    Using A1 and A2 as independent variables and the number of brothers and sisters as dependent variables, we conducted multiple Logit regression analysis. From the table above, we can see that a total of 80 samples participated in the analysis.

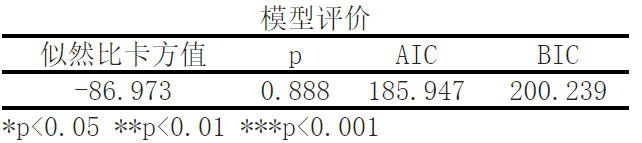
    The results of the likelihood ratio chi square test of the model show that the likelihood ratio chi square value is -86.973, and the significance P value is 0.888>0.05, which does not show significance at the level and can accept the original hypothesis. Therefore, the model is invalid.

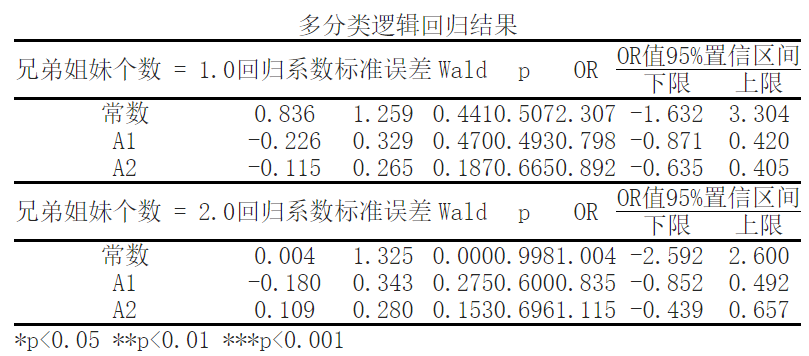
    The significance P value of variable A1 is 0.507>0.05, which is not significant at the level and cannot reject the original hypothesis, so A1 will not have a significant impact on the number of brothers and sisters. The significance P value of variable A2 is 0.493>0.05, which is not significant at the level and cannot reject the original hypothesis, so A2 will not have a significant impact on the number of brothers and sisters.

Interpretation of Results:

Based on the results of the multiple logistic regression model, we draw the following conclusions:

  • When the number of brothers and sisters is 1.0, the regression coefficient of the constant term is 0.836, the standard error is 1.259, and the p value is 0.441. This means that if other independent variables remain unchanged, the probability of the number of brothers and sisters being 1.0 is 0.507. The 95% confidence interval of the regression coefficient is [-1.632, 3.304], indicating a low reliability of the results
  • When the number of brothers and sisters is 2.0, the regression coefficient of the constant term is 0.004, the standard error is 1.325, and the p value is 0.000. This means that when other independent variables remain unchanged, the probability of the number of brothers and sisters being 2.0 is 0.998. The 95% confidence interval of the regression coefficient is [-2.592, 2.600], indicating a low reliability of the results.

Interpretation of results:

By analyzing the results of the multiple logistic regression model, we draw the following conclusions:

  • The independent variables "A1" and "A2" have no significant effect on the number of brothers and sisters. With the other independent variables unchanged, the change of these two independent variables has no significant impact on the probability of "the number of brothers and sisters"

It should be noted that the interpretation of the model results needs to take into account the characteristics of the data and the background of the analysis. In this analysis, the goodness of fit of the model was good, but the influence of independent variables was not significant. Meanwhile, the reliability of the model results needs further verification.

It should be noted that this test is based on the first category as the reference category, not the last category. This result is completely consistent with the results obtained by SPSS software, and SPSSMAX outputs more indicators.


关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。