Principal component analysis is a dimensionality reduction technique used to convert high-dimensional data into low-dimensional data while preserving the main information in the data. It achieves dimensionality reduction by finding the main variance directions in the data and projecting the data onto these main directions.

    Using A1-A5 five column data as analysis variables for principal component analysis, the results showed:

    Using factor analysis for information enrichment research, the first step is to analyze whether the research data is suitable for factor analysis. From the table above, it can be seen that the kmo value is 0.718>0.7, indicating high validity, indicating that the data can be used for factor analysis research. And the data passed the Bartlett sphericity test (p<0.05), indicating that the research data is suitable for factor analysis.

    From the component matrix before rotation in the table above, it can be seen that factor analysis was performed on the input variables, and a total of 2 factors were extracted, indicating that ['A1 ','A2','A3 ','A4','A5 '] these variables can be divided into 2 different dimensions.

    The above table analyzes the situation of factor extraction and the amount of information extracted. From the above table, it can be seen that factor analysis has extracted a total of 2 factors, with feature root values greater than 1. The variance interpretation rates of these 2 factors after rotation are [46.665, 20.669]%, and the cumulative variance interpretation rate is 67.334%.

     SPSSMAX also calculates and outputs the component score coefficient matrix and weight results.

    The comprehensive score can be used to compare the overall competitiveness situation. The higher the comprehensive score value, the stronger the overall competitiveness. This type of application is commonly used in economic and management research, such as comparing the competitive strength of listed companies.

     Factor 1 = -0.506 * A1 + -0.14 * A2 + -0.568 * A3 + -0.501 * A4 + -0.389 * A5

     Factor 2 = 0.203 * A1 + -0.914 * A2 + -0.05 * A3 + -0.141 * A4 + 0.318 * A5

     F=0.862* Factor 1 + F=0.023* Factor 2

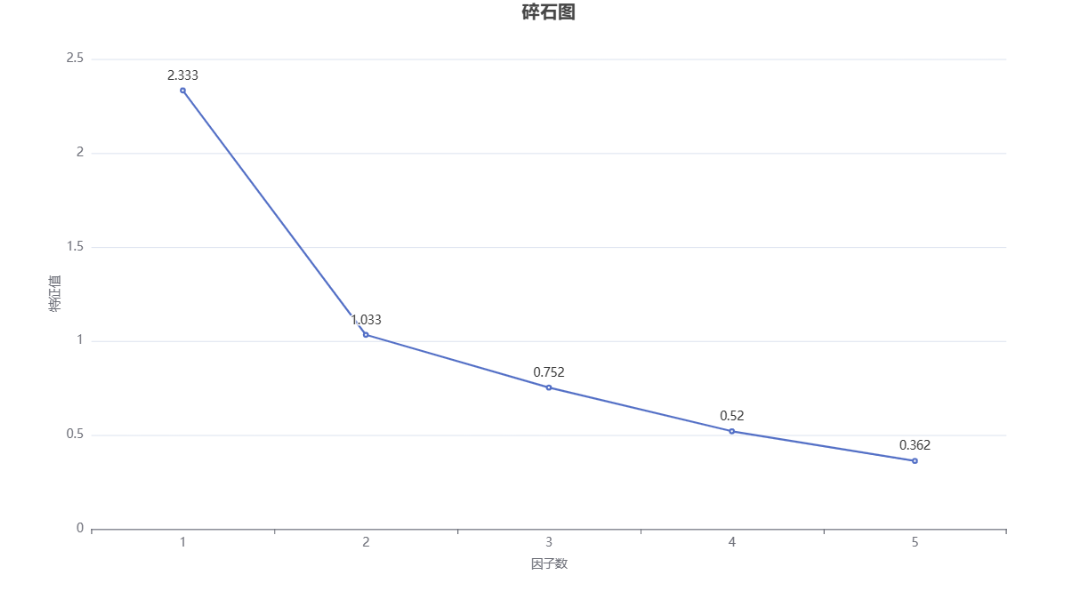
     SPSSMAX also outputs a gravel map, which displays feature roots in graphical form and is mainly used to assist in determining the number of factors.

     Reference:

    [1]Jolliffe, I. T. (2011). Principal component analysis (2nd ed.). Springer.

    [2]Shlens, J. (2014). A tutorial on principal component analysis. arXiv preprint arXiv:1404.1100.

    [3]Abdi, H., & Williams, L. J. (2010). Principal component analysis. Wiley Interdisciplinary Reviews: Computational Statistics, 2(4), 433-459.

    [4]Jackson, J. E. (2005). A user's guide to principal components. John Wiley & Sons.

    [5]Rencher, A. C. (2002). Methods of multivariate analysis. John Wiley & Sons.

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。