二元逻辑回归是一种用于解决二分类问题的方法。在二元逻辑回归中，我们的目标是根据给定的特征，将样本分为两个类别，通常用0和1表示。逻辑回归利用了一种称为逻辑函数（或称为Sigmoid函数）的映射函数，将线性组合的特征映射到一个0-1之间的概率值。通过设定一个阈值，我们可以根据预测的概率值确定样本的分类。

    数据说明：

    背景说明：

    二元逻辑回归是一种用于处理二分类问题的统计模型。它基于输入特征的线性组合，使用一个目标函数（也称为sigmoid函数）对结果进行概率化，从而预测样本属于某一类别的概率。在这个分析中，研究者想要了解是否是独生子女（是或否）是否受到几个自变量（A1、A2）的影响。研究者使用了二元逻辑回归模型来构建预测模型。

    分析结果如下所示：

    将['A1', 'A2']作为自变量，而将是否是独生子女作为因变量进行二元Logit回归分析,从上表可以看出，总共有80个样本参加分析。

     对模型整体有效性进行分析，从上表可知：此处模型检验的原定假设为：是否放入自变量['A1', 'A2']两种情况时模型质量均一样；这里p值大于0.05，因而说明接受原定假设，即说明本次构建模型时，放入的自变量无意义，也即说明本次模型构建没有意义，后续的指标结果等均没有意义。

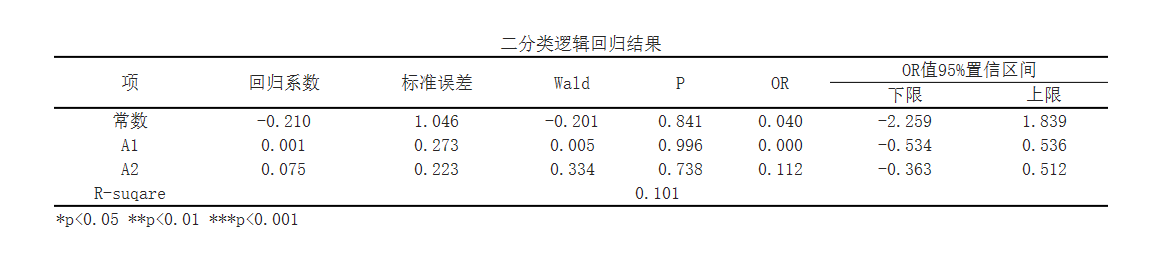
     从上表可知，将[‘A1’, ‘A2’]为自变量，而将是否是独生子女作为因变量进行二元Logit回归分析,从上表可以看出自变量可以解释因变量0.101%的变化原因。结果显示，所有自变量均未对因变量是否是独生子女起显著影响作用（p>0.05）。

    从上表可知：模型公式为：ln(p/1-p) = -0.2101 + 0.0013*A1 + 0.0746*A2(其中p代表是否是独生子女为1 的概率，1-p代表是否是独生子女为0的概率)。

     这里p值大于0.05(Chi=2.49, p=0.778>0.05)，因而说明接受原定假设，即说明本次模型通过HL检验，模型拟合优度较好。

    参考文献：

    [1]姜广辉，张凤荣，陈军伟等.基于Logistic回归模型的北京山区农村居民点变化的驱动力分析． 《 CNKI;WanFang 》，2007

    [2]谢花林，李波.基于logistic回归模型的农牧交错区土地利用变化驱动力分析——以内蒙古翁牛特旗为例． 《 CNKI;WanFang 》，2008

    [3]朱丽，王声湧，范存欣等.高校青年教师亚健康危险因素Logistic回归分析．《 中国公共卫生 》，2003

    [4]王阶，李军，姚魁武，衷敬柏.冠心病心绞痛证候要素和冠脉病变的Logistic回归分析．CNKI;WanFang 》，2007

    [5]庞素琳.Logistic回归模型在信用风险分析中的应用．《 数学的实践与认识 》，2006

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。