岭回归
岭回归(Ridge Regression)是一种用于线性回归分析的正则化方法。它通过对模型的系数进行约束,从而可以降低模型的方差,并在高维数据的情况下可以防止过拟合。岭回归的本质是在损失函数中加入一个正则项,对模型参数进行惩罚,得到的新的损失函数就可以使用梯度下降等方法进行优化。
数据说明:

背景说明:
岭回归分析主要应用于在线性回归模型中存在共线性或样本量较小的情况下。当自变量之间存在高度相关性或样本量不足以支持普通最小二乘法的假设时,岭回归可以通过引入岭惩罚项来解决这些问题。这个分析提供了各个指标变量对因变量的影响程度的评估,并帮助我们理解每个指标变量的贡献。
它在普通最小二乘法的基础上使用了岭惩罚项,以减少模型的方差。它通过引入岭惩罚项来平衡拟合优度和模型复杂度。岭回归可以在存在共线性或样本量小于变量数的情况下提高模型的性能。
在这个分析中,我们使用岭回归分析来研究各个指标变量(包括常数项)对因变量(SAS总分)的影响。非标准化系数表示了指标变量对因变量的平均影响大小。通过95%Bootstrap置信区间,我们可以确定回归系数的范围。t值和对应的p值用于检验回归系数是否显著。
分析结果如下所示:

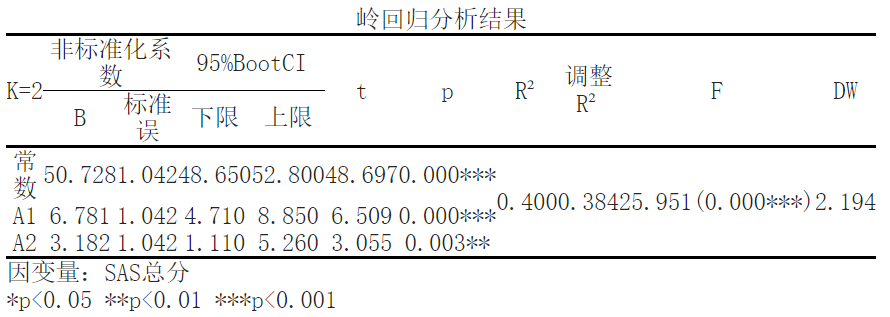
结果显示,将['SAS总分']作为因变量,['A1', 'A2']作为自变量进行岭回归分析,从上表可以看出,在k值为2时;模型R方值为0.4,意味着['A1', 'A2']能解释['SAS总分']的39.954663%变化原因。结果显示,当K值大于等于2时,标准化回归系数趋于稳定。同时,模型的拟合优度R²为0.399,模型表现较好。此时,F检验的显著性P值为0.0<0.05,水平上呈现显著性,拒绝原假设,表明自变量与因变量之间存在着回归关系。
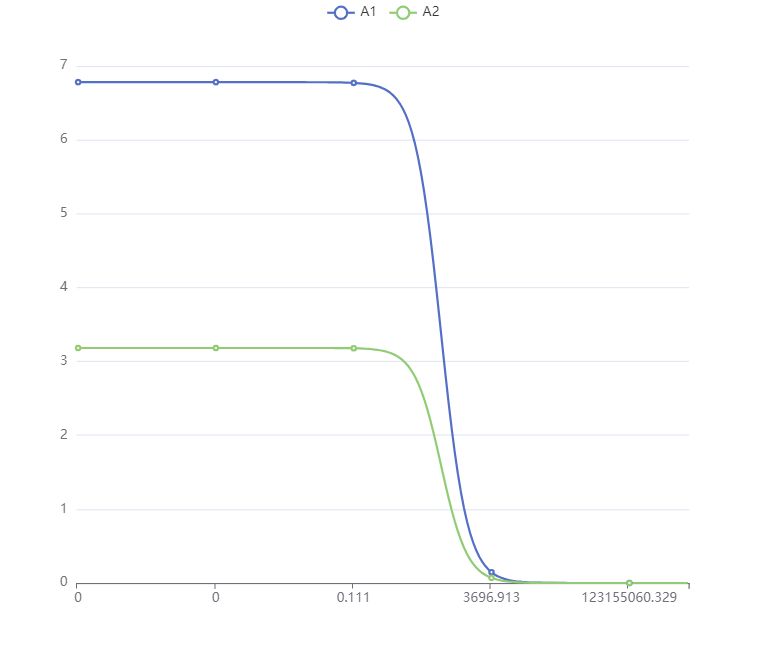
在分析结果中,首先进行了模型评价。似然比检验、AIC(Akaike信息准则)和BIC(贝叶斯信息准则)是用来评估模型的拟合优度和泛化能力的统计指标。
- 似然比检验(Likelihood Ratio Test)用于比较两个或更多模型的拟合优度,这里的似然比检验的值为-294.690。
- AIC和BIC是模型选择的准则,考虑了拟合效果和模型复杂度。AIC的值为595.381,BIC的值为602.564。数值越小表示模型越好。
接下来的部分展示了进行了岭回归分析的结果。岭回归是一种用于处理多重共线性的回归分析方法,它通过引入正则化项(岭项)来控制模型的复杂度,从而提高模型的稳定性和泛化能力。
具体分析结果如下:
- K=2:这里的K表示模型中的自变量个数,即岭回归模型考虑了两个自变量。
- 非标准化系数:给出了自变量的回归系数,这些系数代表自变量对因变量的影响程度。例如,变量A1的回归系数为6.781,变量A2的回归系数为3.182。
- 95%BootCI:给出了回归系数的置信区间,用于估计系数的精度。上下限分别代表了置信区间的边界。
- t和p:t统计量用于检验回归系数是否显著不为零,p值表示系数的显著性水平。例如,常数项的t统计量为25.951,对应的p值为0.000***(显著性水平非常低)。
- R²和调整R²:R²表示模型对观测值的拟合优度,调整R²考虑了自变量个数和样本容量的影响,用于对模型进行比较和选择。在这里,R²为0.400,调整R²为0.384,数值越高表示模型拟合得越好。
- F统计量:F统计量用于检验模型整体拟合优度的显著性。在这里,F统计量为48.697,对应的p值为0.000***。
- DW统计量:Durbin-Watson统计量用于检验模型中是否存在自相关性(误差项之间的相关性)。数值接近2表示没有自相关,这里的DW统计量为2.194。
最后,给出了因变量为"SAS总分"的定义,"*p<0.05 **p<0.01 ***p<0.001"表示统计显著性水平。
综上所述,岭回归分析通过引入正则化项,处理多重共线性问题,得到了一组自变量对于因变量的回归系数。结果表明,在考虑两个自变量的情况下,模型在显著性水平较低下具有良好的拟合优度和预测能力。
参考文献:
[1]Tikhonov, A. N. (1943). "On the stability of inverse problems". Dokl. Akad. Nauk. USSR.7: 386–389.
[2]Hoerl, A.E.; Kennard, R.W. (1970). "Ridge Regression: Biased Estimation for Nonorthogonal Problems". Technometrics.12 (1): 55–67.
关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。
