描述统计

描述统计是通过图表或数学方法，对数据资料进行整理、分析，并对数据的分布状态、数字特征和随机变量之间关系进行估计和描述的方法。

描述统计分为集中趋势分析和离中趋势分析。

集中趋势分析主要靠平均数、中数、众数等统计指标来表示数据的集中趋势。

离中趋势分析主要靠全距、四分差、平均差、方差、标准差等统计指标来研究数据的离中趋势。

数据说明：

分析表格如下所示：：

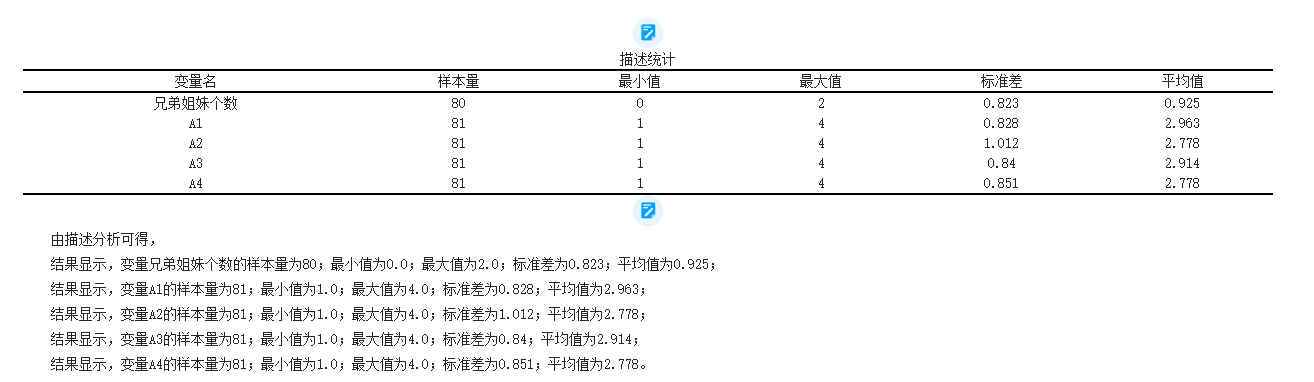
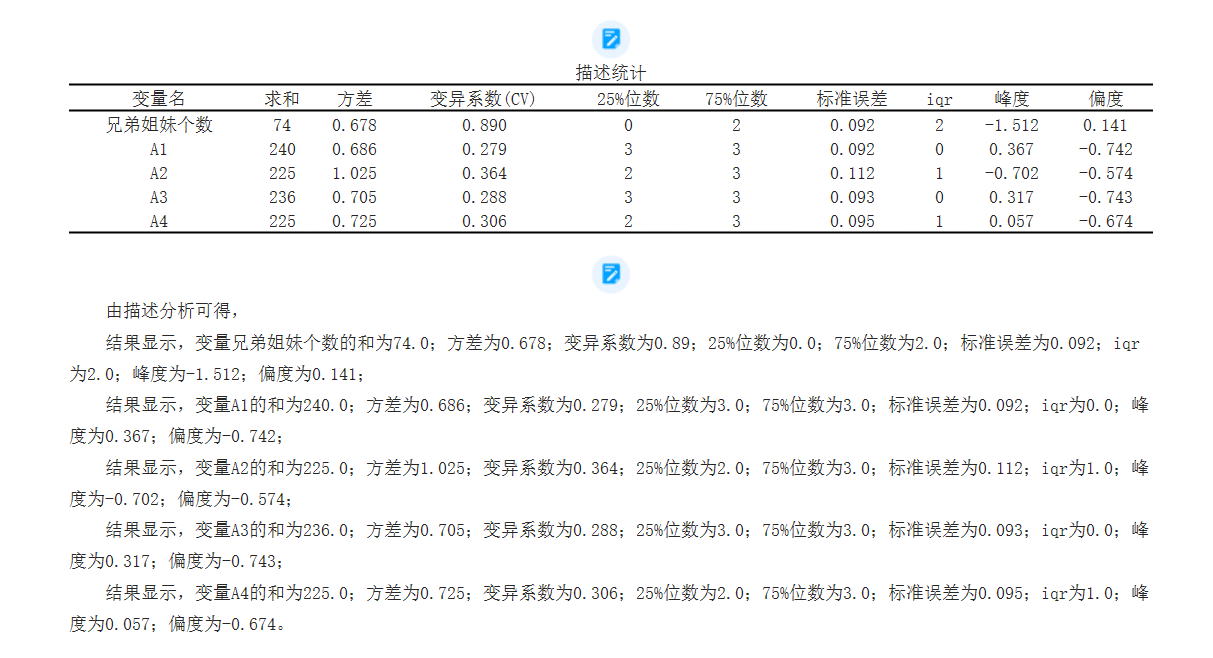
下面是对各个指标的详细解释：

1. 求和：求和指标表示将一组数据中所有数值相加的结果。它是一种简单的统计量，用于表示总体或样本的总量。

2. 方差：方差是一种度量数据分散程度的指标。它表示数据观测值与其平均值之间的差异程度。方差越大，数据的离散程度越大。

3. 变异系数（CV）：变异系数也是一种度量数据离散程度的指标，它是方差与均值的比值。变异系数可以比较不同样本或总体间的离散程度。较小的变异系数表示数据相对较稳定，较大的变异系数则表示数据相对较不稳定。/5）。

4. 25%位数和75%位数：这两个指标也被称为四分位数。25%位数，又称第一四分位数，表示数据集中25%的观测值位于该值以下；75%位数，又称第三四分位数，表示数据集中75%的观测值位于该值以下。四分位数可以用来描述数据的分布情况和发现异常值。

5. 标准误差：标准误差是指样本均值和总体均值之间的差异。它是一种度量样本均值估计的精确度的指标。标准误差越小，样本均值估计越精确。

6. IQR：IQR即四分位间距，是指75%位数与25%位数之差。它可以用来度量数据的离散程度。IQR较大表示数据分布较广，IQR较小表示数据分布较集中。

7. 峰度：峰度是衡量数据分布形态陡峭或平坦程度的指标。正态分布的峰度为3，如果峰度大于3，则数据呈现尖峭的分布；如果峰度小于3，则数据呈现平坦的分布。

8. 偏度：偏度是衡量数据分布对称性的指标。偏度为0表示数据分布完全对称，偏度大于0表示数据分布右偏（正偏），偏度小于0表示数据分布左偏（负偏）。

分析图形如下所示：

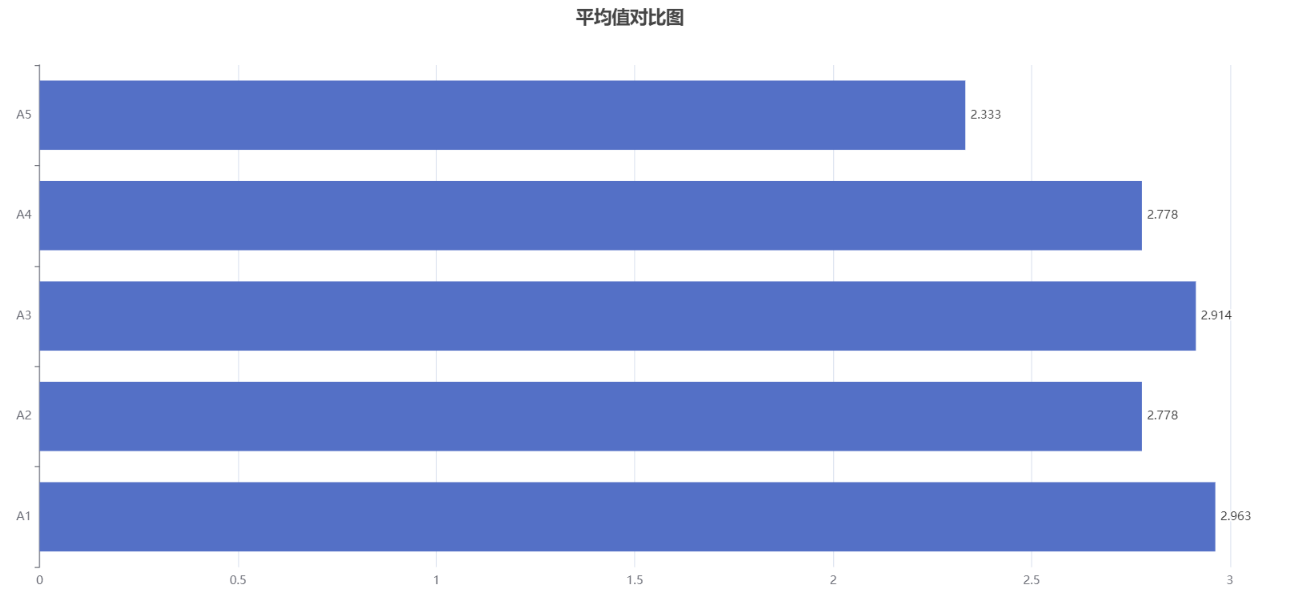
柱状图是一种常见的数据可视化方式，用于比较不同类别或组之间的数据。它由一系列垂直或水平的矩形条组成，每个矩形条的长度表示数据的大小。

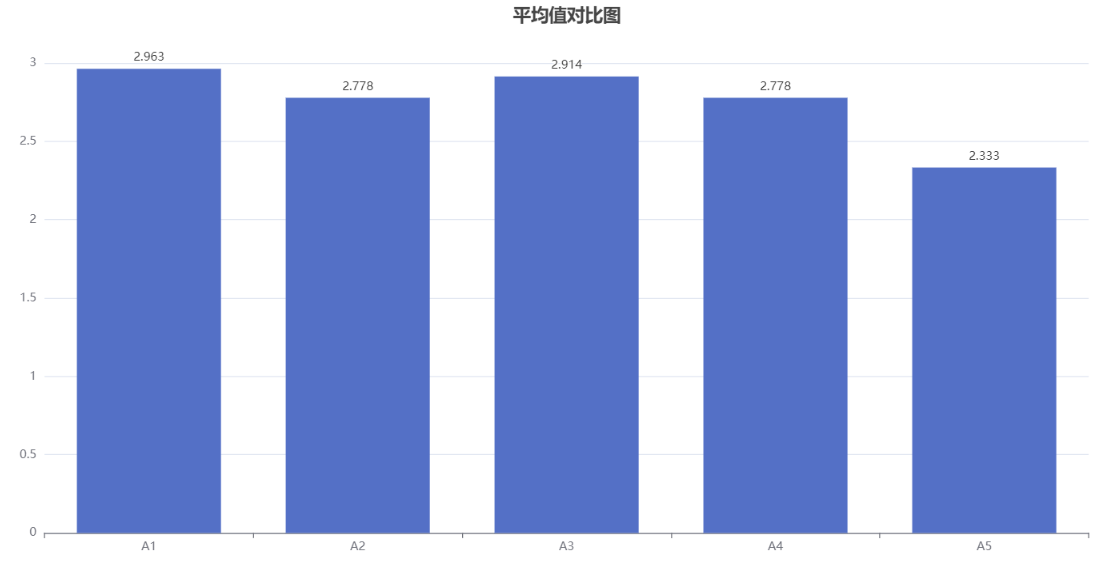
二维条形图是一种常用的数据可视化方式，用于展示不同类别或组的数量或比较。它由水平和垂直两个轴组成，其中水平轴表示不同的类别或组，垂直轴表示数量或比例。每个类别或组用一个条形表示，其高度或长度与对应的数值相关联。

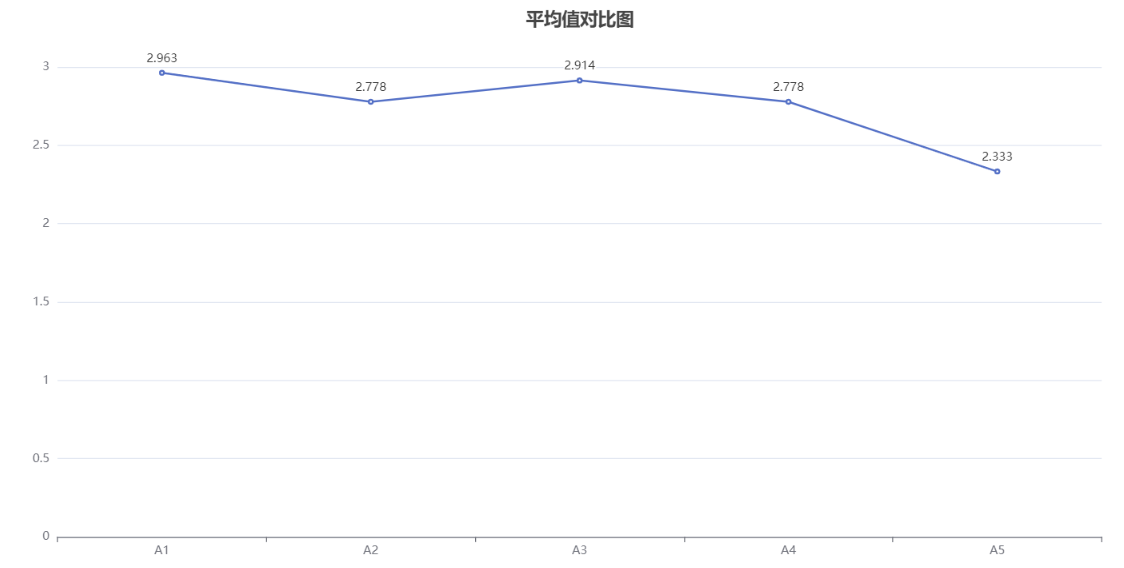
折线图是一种常见的数据可视化方式，用于显示数据随着时间、顺序或其他连续变量的变化趋势。它由一条或多条折线组成，每条折线表示不同变量随着自变量的变化而变化的趋势。

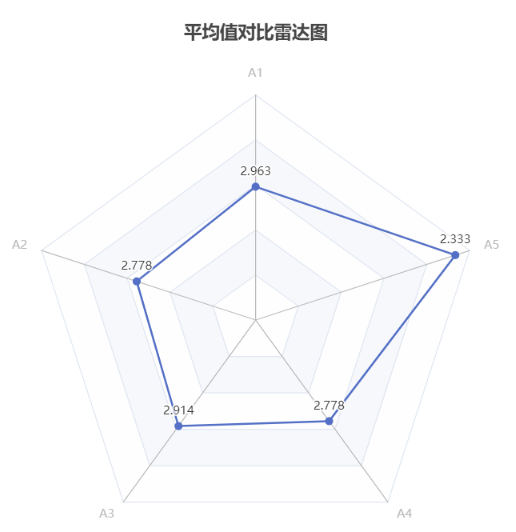
雷达图是一种用于比较多个变量或多个选项之间的关系的数据可视化方式。它由一个中心点和多个等距的轴线组成，每个轴线表示一个变量，从中心点延伸到不同方向的长度表示该变量的值。