(偏)自相关用于检测时间序列数据中的自相关性，即当前观测值和过去观测值之间的相关性。它可以帮助确定时间序列数据的自相关模式，从而选择适当的时间序列模型。

    数据说明：

    背景说明：

    自相关是用来衡量时间序列数据中当前观测值与之前观测值之间的相关性。AC值表示当前观测值与特定滞后阶数之前观测值的相关性，而PAC值表示通过消除其他滞后阶数的干扰后，当前观测值与特定滞后阶数之前观测值的相关性。在这个例子中，我们进行了(偏)自相关检验，通过计算滞后阶数为1到5的自相关系数(AC值)和偏自相关系数(PAC值)，以及相应的Q统计量和p值来评估时间序列数据的自相关性。

    分析结果如下所示：

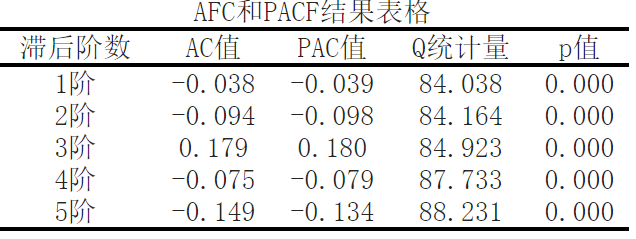
    在这个例子中，我们可以观察到以下几个方面：

    AC值和PAC值的正负：AC值和PAC值的正负可以告诉我们关于时间序列数据中的正相关或负相关关系。负值表示负相关，即当前观测值较大时，之前的观测值较小；正值表示正相关，当前观测值较大时，之前的观测值也较大。

    Q统计量和p值：Q统计量是在假设时间序列数据没有自相关性的情况下，检验观测值与滞后观测值之间的相关性的统计量。p值表示给定假设的条件下，观测值与滞后观测值之间存在显著相关性的概率。在这里，p值均为0.000，说明观测值与滞后观测值之间存在显著的相关性。

    自相关函数图(Autocorrelation Function, AFC)是描述时间序列数据自相关性的图形。该图显示了滞后阶数对应的AC值的变化。根据给定的滞后阶数，AC值越接近1，表示当前观测值与滞后观测值之间存在较强的相关性。

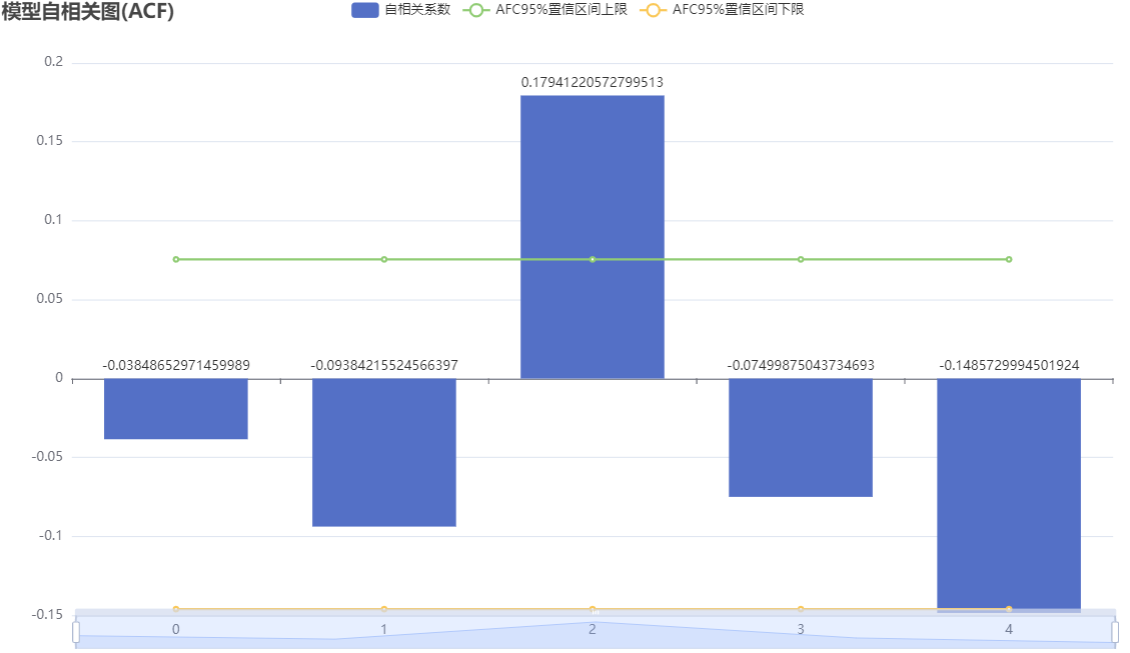
    上图展示了自相关图(ACF)，包括系数、置信上限和置信下限。 横轴代表延迟数目，纵轴代表自相关系数。 自相关(ACF)图在q阶进行截尾，偏自相关(PACF)图拖尾，ARMA模型可简化为MA(q)模型。 倘若自相关与偏自相关图均拖尾，可结合PACF、ACF图中最显著的阶数（最小值）作为p、q值。

    倘若自相关与偏自相关图均截尾，可以选择更换更高的差分，或不适合建立ARMA模型。 截尾是在置信区间内，ACF或PACF在某阶后就恒等于零（或在0附近随机波动）。 拖尾是在置信区间内，ACF或PACF始终有非零取值，不呈现在某阶后就恒等于零（或在0附近随机波动）。

    部分自相关函数图(Partial Autocorrelation Function, PACF)用于评估当前观测值与特定滞后阶数之前观测值之间的相关性。PACF图显示了滞后阶数对应的PAC值的变化。与AFC图不同，PACF图观察的是消除了其他滞后阶数的干扰后的相关性。

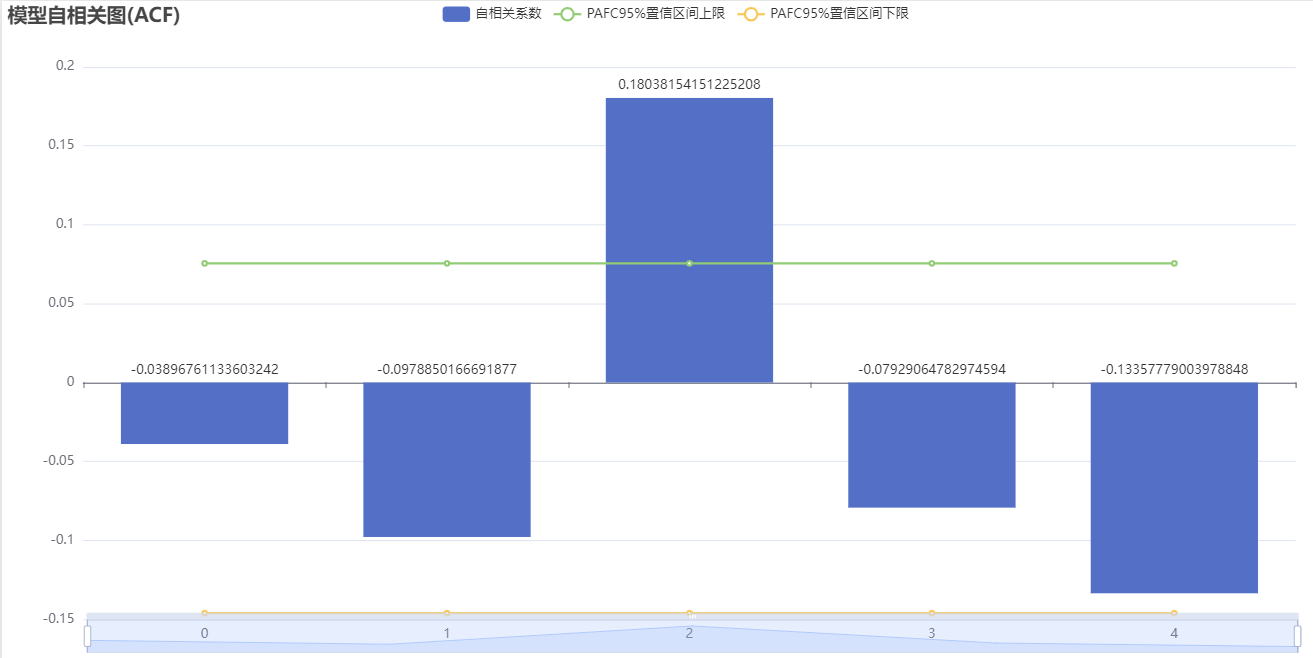
    上图展示了偏自相关图(PACF)，包括系数，置信上限和置信下限。 偏自相关(PACF)图在p阶进行截尾，自相关(ACF)图拖尾，ARMA模型可简化为AR(p)模型。 倘若自相关与偏自相关图均拖尾，可结合PACF、ACF图中最显著的阶数(最小值)作为p、q值。

    倘若自相关与偏自相关图均截尾，可以选择更换更高的差分，或不适合建立ARMA模型。 截尾是在置信区间内，ACF或PACF在某阶后就恒等于零(或在0附近随机波动)。 拖尾是在置信区间内，ACF或PACF始终有非零取值，不呈现在某阶后就恒等于零(或在0附近随机波动)。

    参考文献：

    [1]Box, G. E., Jenkins, G. M., Reinsel, G. C., & Ljung, G. M. (2015). Time series analysis: Forecasting and control (5th ed.). John Wiley & Sons.

    [2]Wei, W. W. S. (2006). Time series analysis: Univariate and multivariate methods. Pearson Education.

    [3]Lutkepohl, H. (2017). New introduction to multiple time series analysis. Springer.

    [4]Cryer, J. D., & Chan, K. S. (2008). Time series analysis: With applications in R (2nd ed.). Springer.[5]Hamilton, J. D. (1994). Time series analysis. Princeton University Press.  

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。