聚类分析（K-means聚类）是一种基于中心的聚类算法，根据使每个样本与其类的中心或平均值之间的距离之和最小化原则，迭代地将样本自动划分为K类，始终追求簇内差异小、簇间差异大的目标，其中差异由样本点到其所在簇的质心的距离衡量。

    数据说明：

    背景说明：

    关于K-means聚类分析，它是一种常用的无监督学习方法，用于将数据样本划分成不同的类别。它通过最小化各样本点到类别中心的距离来进行聚类。具体而言，它将样本点分配到离其最近的类别中心，然后更新类别中心，不断迭代直到收敛。K-means聚类分析通常用于探索数据中的潜在模式和结构，并对数据进行分类。

    它可应用于多个领域，如市场分割、图像分析和生物学研究等。它的一个优点是简单且易于理解，但也存在一些限制，比如对初始类别中心的选择敏感。在本分析中，使用了K-means聚类分析来根据变量的特征将数据分成两个不同的类别，并进行了显著性检验来评估变量在这些类别之间的差异。以上结果提供了关于每个变量在不同聚类类别之间的差异性的详细解释。

    分析结果如下所示：

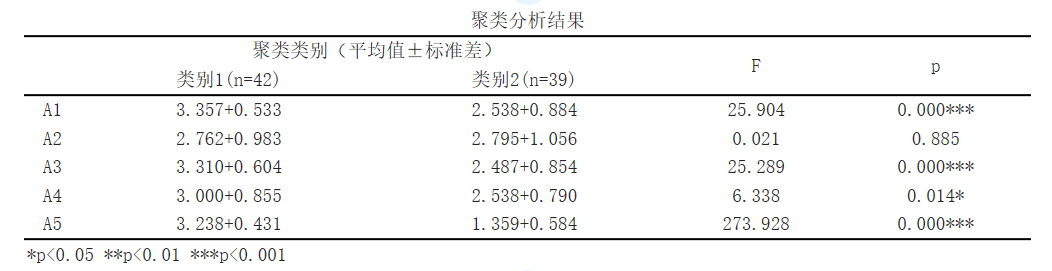
    对于变量 A1, 显著性P值为 0.0<0.05， 水平上呈现显著性，拒绝原假设，说明变量 A1 在聚类分析划分的类别之间存在显著性差异。

    对于变量 A2, 显著性P值为 0.885>0.05, 水平上呈现不显著性，接受原假设，说明变量 A2 在聚类分析划分的类别之间没有显著性差异。

    对于变量 A3, 显著性P值为 0.0<0.05， 水平上呈现显著性，拒绝原假设，说明变量 A3 在聚类分析划分的类别之间存在显著性差异。

    对于变量 A4, 显著性P值为 0.014<0.05， 水平上呈现显著性，拒绝原假设，说明变量 A4 在聚类分析划分的类别之间存在显著性差异。

    对于变量 A5, 显著性P值为 0.0<0.05， 水平上呈现显著性，拒绝原假设，说明变量 A5 在聚类分析划分的类别之间存在显著性差异。

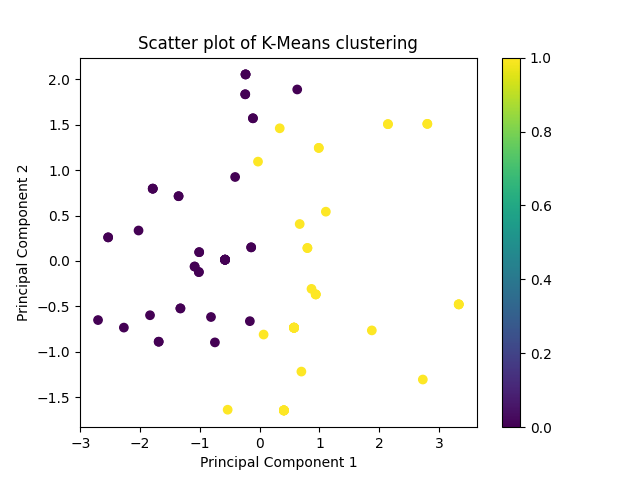
关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。