Fisher精确检验是一种非参数统计方法，用于比较两个分类变量的分布之间的差异。它适用于小样本或离散数据的情况，不要求满足正态分布假设。

    Fisher精确检验是由统计学家Ronald Fisher提出的一种非参数统计检验方法，用于比较两个分类变量之间的关联性。它特别适用于小样本数据或者存在某些特殊条件的数据。该检验可以帮助我们确定两个变量之间是否存在显著的关联，而不依赖于数据的分布假设。

    在这个Fisher精确检验结果中，我们对两个因素进行了分析：是否是独生子女和性别。

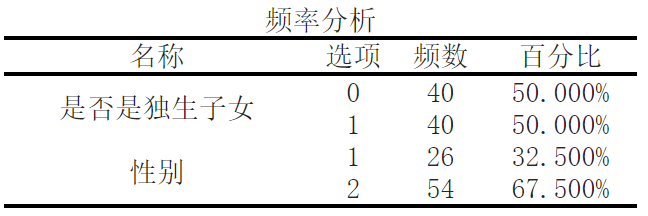
     由频率分析可知，是否是独生子女中0.0有40个，占比50.00%；是否是独生子女中1.0有40个，占比50.00%。

     性别中1.0有26个，占比32.50%；性别中2.0有54个，占比67.50%。

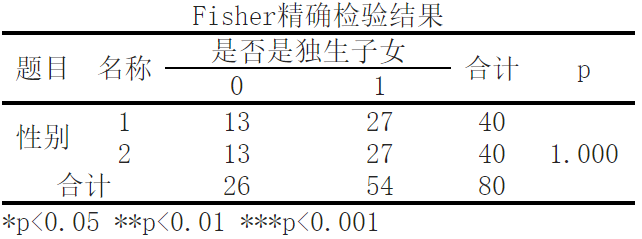
    P值大于等于0.05，不呈现显著性，接受原假设，则说明分类变量X与分类变量Y之间不存在显著性差异

    在这个Fisher精确检验结果中，我们对两个因素进行了分析：是否是独生子女和性别。 Fisher精确检验是一种用于比较两个分类变量之间是否存在显著关联的统计检验方法。

    在这个检验结果中，我们可以看到性别和是否是独生子女之间的关联情况。在这个例子中，p值为1.000，大于通常的显著性水平0.05。因此，我们无法得出两个因素之间存在显著关联的结论。

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。