Poisson分布是统计学中一种离散概率分布，用于描述某个固定时间或空间间隔内事件发生的次数。它假设事件发生的平均速率没有变化，并且事件之间是独立发生的。

    数据说明：

    背景说明：Poisson分布是一种用来描述某一特定时间段或空间单位内发生某事件次数的概率分布。在这里，我们使用Poisson分布来检验实际频数与期望频数之间是否存在显著差异。在这个Poisson检验表中，我们对两个名称为A1和A2的选项进行了Poisson分布检验。

     分析结果如下所示：

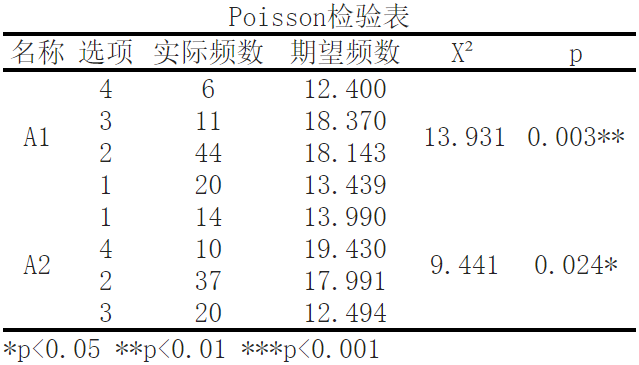
     泊松检验的结果显示，基于变量A1，显著性P值为0.003<0.05，水平上呈现显著性，因此拒绝原假设，因此数据不服从泊松分布。

     泊松检验的结果显示，基于变量A2，显著性P值为0.024<0.05，水平上呈现显著性，因此拒绝原假设，因此数据不服从泊松分布。

    首先，让我们看一下A1选项的结果。根据实际观测的频数，4个观测值出现了6次，11个观测值出现了18次，44个观测值出现了20次，20个观测值出现了13次。通过计算，得到了每个观测值的期望频数，并用X²统计量来评估实际观测频数与期望频数之间的差异程度。在这种情况下，计算得到的X²为13.931，对应的p值为0.003**。这意味着，如果我们假设实际观测数据符合Poisson分布，那么观察到的数据与期望数据之间的差异是高度显著的。

    接下来，我们来看A2选项的结果。根据实际观测的频数，1个观测值出现了14次，10个观测值出现了19次，37个观测值出现了17次，20个观测值出现了12次。计算得到的X²为9.441，对应的p值为0.024*。与A1选项类似，这表明实际观测数据与期望数据之间存在显著差异。

    综上所述，Poisson分布检验用于评估观测数据与Poisson分布的拟合程度。它通过计算X²统计量和相应的p值来判断实际观测数据是否与期望数据之间存在显著差异。在这个检验表中，我们发现A1选项和A2选项的实际观测数据与Poisson分布之间的差异是显著的。

    参考文献：

    [1]Law, A. M., & Kelton, W. D. (2015). Simulation modeling and analysis. McGraw-Hill Education.

    [2]Ross, S. M. (2019). A first course in probability. Pearson Education.

    [3]Walpole, R. E., Myers, R. H., Myers, S. L., & Ye, K. (2011). Probability & statistics for engineers & scientists. Pearson Education.

    [4]Mood, A. M., Graybill, F. A., & Boes, D. C. (2015). Introduction to the theory of statistics. McGraw-Hill Education.

    [5]Gujarati, D. N., & Porter, D. C. (2009). Basic econometrics (5th ed.). McGraw-Hill International.

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。