三次曲线回归分析也是一种回归分析方法，用于研究两个变量之间的关系。在三次曲线回归分析中，我们假设两个变量之间存在一个三次方程的关系，而分析数据以确定三次方程的系数。然后可以使用这个三次方程来预测一个变量的值，给定另一个变量的值。与二次曲线回归分析类似，三次曲线回归分析通常用来研究自然现象的变化趋势或市场趋势等。需要注意的是，三次曲线回归分析相对于二次曲线回归分析在方程复杂度上更高，因此需要更多的数据点来确定系数。

    背景说明：

    在这个研究中，我们关注了自变量A1对于因变量A2的影响，并采用了三次曲线回归方法。这些变量是通过调查问卷获得的数据，用于评估参与者在某个特定问题上的特征或行为。三次曲线回归是一种统计分析方法，用于建立自变量与因变量之间呈三次多项式关系的模型。相比于简单的线性回归模型，三次曲线回归模型可以更准确地描述自变量对因变量的影响，因为它考虑了三次项和二次项的效应。具体来说，三次曲线回归会对数据拟合一个三次多项式模型，以最小化模型与实际观测点之间的误差。

    分析结果如下所示：

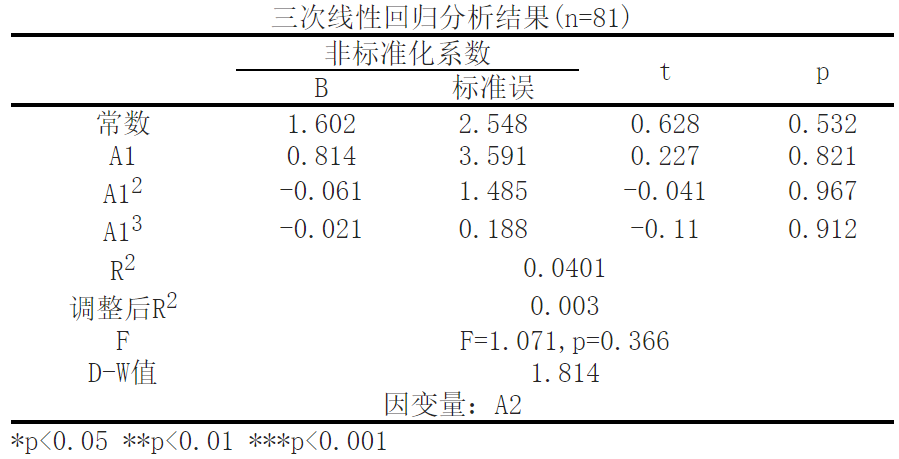
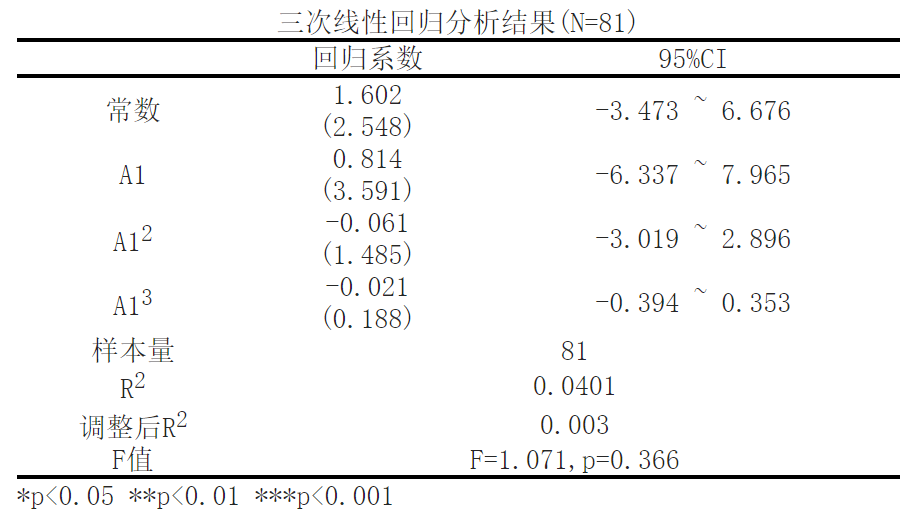
     由线性回归分析可知，将A2作为因变量，['A1']及其平方指标与三次方指标作为自变量进行三次回归分析，从上表可以看出，模型公式为：A2 = 1.602 + 0.814*A1 - 0.061*A1_square - 0.021*A1_cube；模型R方值为0.0401,意味着['A1']及其平方指标与三次方指标能解释A2的4.01%变化原因。A2 = 1.602 + 0.814*A1 - 0.061*A1_square - 0.021*A1_cube

    参考文献：

    [1]Golub, G. H., & Van Loan, C. F. (2013). Matrix computations (4th ed.). Johns Hopkins University Press.

    [2]Liu, X., Zhu, X., Li, Z., & Li, X. (2017). A simulation comparison of inverse distance weighting and cubic spline interpolation for DEM generation. Journal of Earth Science, 28(6), 1089-1096.

    [3]Fernández-Hernández, J., García-Sánchez, Á., & Moya-Gómez, B. (2015). Local forecasting methods based on regression models for time series modeling and prediction. Neurocomputing, 149(PB), 1224-1232

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。