分层回归是一种统计分析方法，用于解决样本存在层级结构的数据分析问题。在分层回归中，数据被分为不同的层级或群组，每个层级内的个体具有相似的特征或属性。

    分层回归方法根据数据结构的特点，调整了回归模型的参数估计和推断方法。通过考虑层级结构，分层回归可以更准确地估计参数、检验效应和进行预测。

    数据说明：

    背景说明：

    在这个研究中，我们关注指标A1、A2、A3和A4对因变量A5的影响。这些指标是通过1到5分量表题获得的数据，用来评估参与者对某个特定问题的态度或观点。为了分析这些变量之间的关系，我们使用了分层回归方法。分层回归是一种统计分析方法，可以同时考虑多个自变量对因变量的影响，并将自变量按照不同的层次进行组织和分析。具体来说，在我们的研究中，我们将自变量A1和A2放置在第一层，这意味着它们可能直接影响因变量A5。自变量A3和A4放置在第二层，我们假设它们通过某种中介机制对因变量A5产生影响。

    分析结果如下所示：

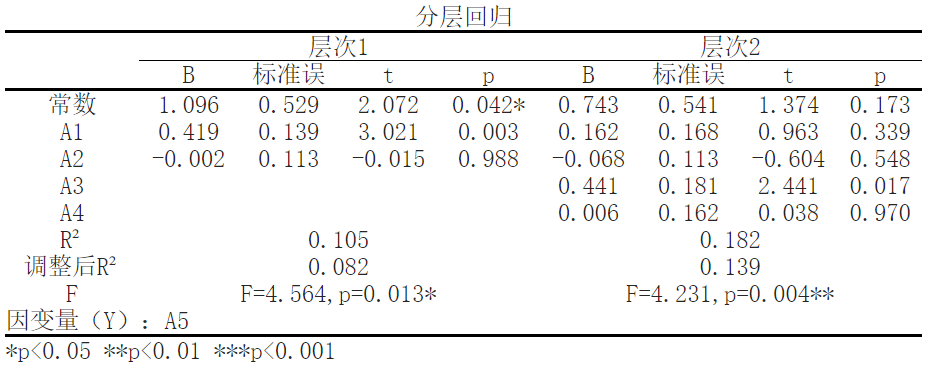
    结果显示，将A5作为因变量，['A1', 'A2']作为自变量，建立自变量和因变量的多元回归模型，R2(RSquare) 代表回归模型中自变量对因变量变异的解释程度，是分析回归结果的开始，数据显示；模型R方值为0.1048,意味着['A1', 'A2']可以解释A5的10.48%变化原因，通过F检验来判断回归模型的回归效果，即检验因变量与所有自变量之间的线性关系是否显著，也可以用来检验模型的统计学意义。由结果可得F值为4.564，P值为0.013，模型公式为：A5 = 1.096 + 0.419*A1 - 0.002*A2。A1对A5存在显著正影响作用，beta值为0.419，p值为0.0034(p<0.05)。

    结果显示，将A5作为因变量，['A1', 'A2', 'A3', 'A4']作为自变量，建立自变量和因变量的多元回归模型，R2(RSquare) 代表回归模型中自变量对因变量变异的解释程度，是分析回归结果的开始，数据显示；模型R方值为0.1821,意味着['A1', 'A2', 'A3', 'A4']可以解释A5的18.21%变化原因，通过F检验来判断回归模型的回归效果，即检验因变量与所有自变量之间的线性关系是否显著，也可以用来检验模型的统计学意义。由结果可得F值为4.231，P值为0.004，模型公式为：A5 = 0.743 + 0.162*A1 - 0.068*A2 + 0.441*A3 + 0.006*A4。A3对A5存在显著正影响作用，beta值为0.4406，p值为0.017(p<0.05)。

    需要注意R²和调整后R²。它们用来评估回归模型的解释能力，分别为0.105和0.082（第一层）以及0.182和0.139（第二层）。这表示自变量解释了总体方差的一定比例，但仍有一些未解释的方差存在。

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。