层次聚类通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。层次聚类的好处是不需要指定具体类别数目的，其得到的是一颗树，聚类完成之后，可在任意层次横切一刀，得到指定数目的簇。

    对A1，A2，A3，A4，A5变量，共81个样本进行系统聚类，采用组间联结的聚类方法，以欧式距离为区间进行聚类分析，生成聚类谱系图。

    数据说明：

    背景说明：

    在这个分析中，我们使用层次聚类分析得到了一个谱系图，用于显示数据样本之间的相似性和差异性。下面是谱系图的详细解释：

    谱系图如下所示：

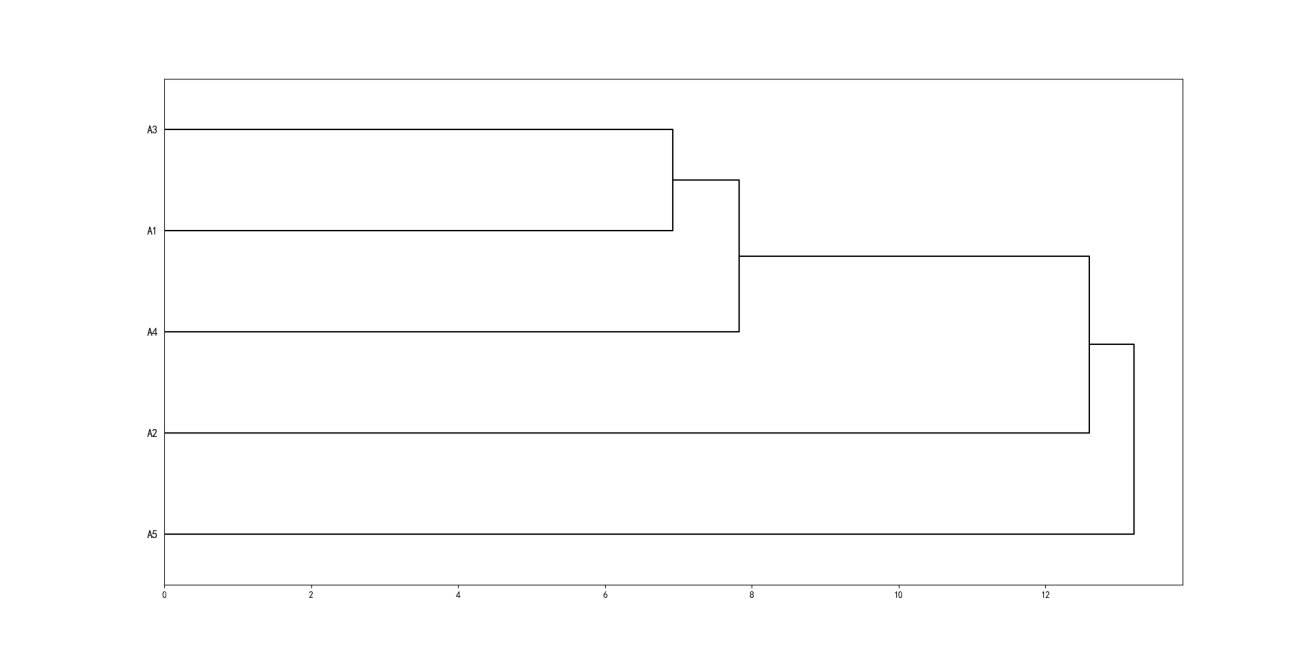
    谱系图是一种图形化表示数据样本之间聚类关系的工具。它显示了数据样本之间的相似性和差异性，并以树状结构的方式呈现。谱系图的根节点代表所有样本的初始聚类，而叶节点代表单个样本。通过观察谱系图的分支和连接，我们可以确定聚类之间的相似性和差异性。 对于层次聚类分析，它是一种无监督学习方法，用于将数据样本进行层次化的聚类。它通过计算样本之间的距离或相似性来构建聚类树。具体而言，层次聚类分析可以分为两种类型：凝聚型和分裂型。

    凝聚型层次聚类从每个样本作为一个独立的聚类开始，然后逐步合并最相似的聚类，直到形成一个大的聚类。分裂型层次聚类从所有样本作为一个大的聚类开始，然后逐步分裂为更小的聚类，直到每个样本都成为一个独立的聚类。

    层次聚类分析通常用于探索数据中的潜在模式和结构，并生成可视化的谱系图来表示聚类关系。谱系图可以帮助我们理解数据样本之间的相似性和差异性，并确定聚类的数量和结构。它在多个领域中都有应用，如生物学、社会科学和市场研究等。

    在本分析中，我们使用层次聚类分析得到了一个谱系图，用于显示数据样本之间的聚类关系。谱系图提供了关于聚类之间的相似性和差异性的详细解释。通过观察谱系图的结构，我们可以确定聚类之间的划分点，从而确定最终的聚类数量和结构。

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。