主成分分析是一种降维技术，用于将高维数据转换为低维数据，同时保留数据中的主要信息。它通过找到数据中的主要方差方向来实现降维，并将数据投影到这些主要方向上。

    将A1-A5五列数据作为分析变量进行主成分分析，结果显示：

    使用因子分析进行信息浓缩研究，首先分析研究数据是否适合进行因子分析，从上表可以看出：kmo数值为0.718>0.7，效度很高,意味着数据可用于因子分析研究。以及数据通过Bartlett 球形度检验(p<0.05)，说明研究数据适合进行因子分析。

    从上表旋转前的成分矩阵可知：对所输入的变量进行因子分析，一共提取出了2个因子，说明['A1', 'A2', 'A3', 'A4', 'A5']这些变量一共可以被划分成为2个不同维度。

    上表格针对因子提取情况，以及因子提取信息量情况进行分析，从上表可知：因子分析一共提取出2个因子，特征根值均大于1，此2个因子旋转后的方差解释率分别是[46.665, 20.669]%，累积方差解释率为67.334%。

     SPSSMAX还计算和输出了成份得分系数矩阵及权重结果。

    综合得分可用于对比综合竞争力情况，综合得分值越高，此时综合竞争力越强。此类应用常见于经济、管理类研究，比如上市公司的竞争实力对比。

     Factor 1 = -0.506 * A1 + -0.14 * A2 + -0.568 * A3 + -0.501 * A4 + -0.389 * A5

     Factor 2 = 0.203 * A1 + -0.914 * A2 + -0.05 * A3 + -0.141 * A4 + 0.318 * A5

     F=0.862* Factor 1 + F=0.023* Factor 2

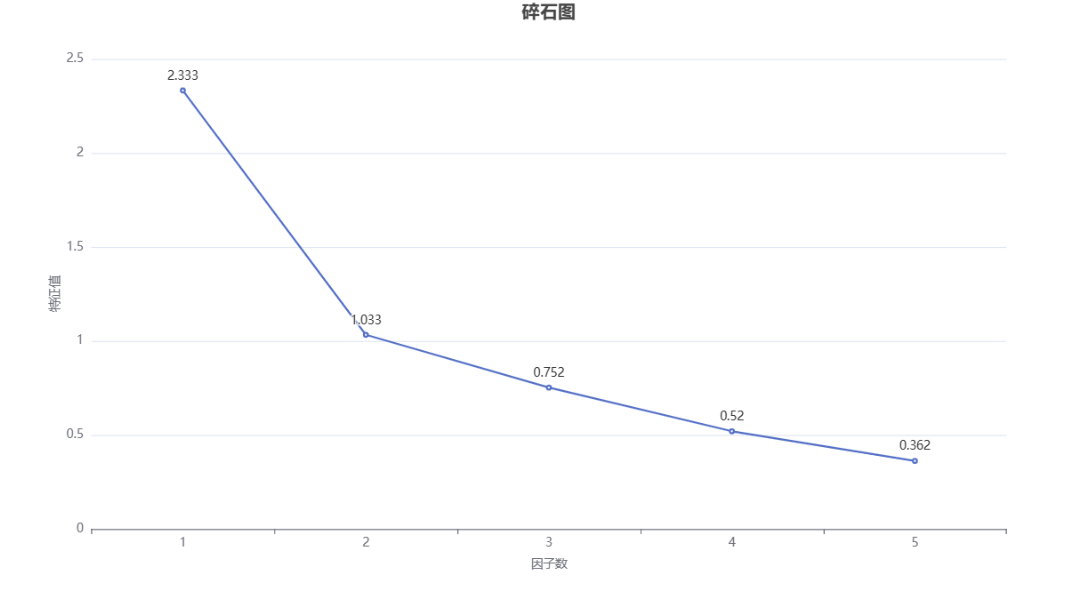
     SPSSMAX还输出了碎石图，碎石图是将特征根以图示形式展示，主要用于辅助判断因子个数。

     参考文献：

    [1]Jolliffe, I. T. (2011). Principal component analysis (2nd ed.). Springer.

    [2]Shlens, J. (2014). A tutorial on principal component analysis. arXiv preprint arXiv:1404.1100.

    [3]Abdi, H., & Williams, L. J. (2010). Principal component analysis. Wiley Interdisciplinary Reviews: Computational Statistics, 2(4), 433-459.

    [4]Jackson, J. E. (2005). A user's guide to principal components. John Wiley & Sons.

    [5]Rencher, A. C. (2002). Methods of multivariate analysis. John Wiley & Sons.

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。