方差分析(Analysis of Variance，简称ANOVA)，又称“变异数分析”或“F检验”，用于两个及两个以上样本均数差别的显著性检验。 由于各种因素的影响，研究所得的数据呈现波动状。造成波动的原因可分成两类，一是不可控的随机因素，另一是研究中施加的对结果形成影响的可控因素，用于两个及两个以上样本均数差别的显著性检验。

    数据说明：

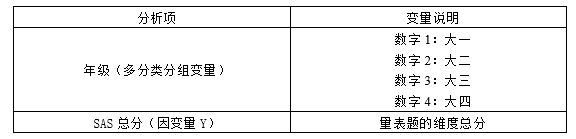
    背景说明：

    方差分析是一种用于比较两个或多个样本平均值差异的统计方法。在这个例子中，我们研究了不同年级（1、2、3、4）的学生在SAS总分上的表现情况。方差分析可以帮助我们了解不同年级之间是否存在显著差异，以及哪些项目在不同年级之间具有显著差异。这些结果对于了解学生学业发展和课程安排具有重要意义。

    分析结果如下所示：

     从上表可知，对SAS总分进行方差分析(全称为单因素方差分析)，结果显示,其F值为0.365，p值为0.779，说明不同组别下的SAS总分之间不存在显著差异（p>0.05）。

    每个指标的详细解释：

    1. 差异：组间组内差异。

    2. 平方和：平方和表示不同组别（年级）的数据之间的总和平方。这个值用于计算方差以及后续的F值。

    3. 自由度：自由度表示在方差分析中可以自由变动的数据个数。对于组间差异，自由度为组别数减去1；对于组内差异，自由度为总体总数减去组别数。

    4. 均方：均方是平方和与自由度的比值，用于评估差异的程度。在方差分析中，我们计算了组间均方和组内均方。

    5. F值：F值用来判断组间差异的显著性水平。它是组间均方与组内均方的比值。在这个例子中，我们计算了每个项目的F值。

    6. p值：p值表示F值的显著性水平。它反映了差异的统计显著性。在这个例子中，我们给出了每个项目的p值。

    参考文献：

    [1] 中国科学院数学研究所统计组 ．方差分析 ：科学出版社 ，1977

    [2] 刘仁权．spss统计软件．北京：中国中医药出版社，2007：50

    [3] 贾俊平，何晓群，金勇进 著 ．统计学：中国人民大学出版社 ，2015

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。