有序逻辑回归（Ordered Logistic Regression），也称为有序多项Logit模型（Ordered Multinomial Logit Model），是一种用于处理有序分类变量的统计分析方法。它是逻辑回归的扩展形式，适用于因变量有多个有序类别的情况。

    有序逻辑回归的目标是建立一个模型，以预测有序分类变量的类别。这些类别通常具有一定的顺序关系，例如"非常不满意"、"不满意"、"一般满意"、"非常满意"。有序逻辑回归使用了一个潜在的连续变量，该变量的值与每个类别之间的阈值相关联。模型通过估计这些阈值，来确定潜在变量的范围，从而将观测值映射到相应的类别。

    有序逻辑回归的数学模型基于多项Logit模型，其中应用了一个累积分布函数（Cumulative Distribution Function，CDF）。该函数描述了每个类别的概率与潜在变量之间的关系。常用的CDF函数包括logit函数、probit函数和cloglog函数等。

    对于有序逻辑回归的建模过程，通常使用最大似然估计方法来估计模型的参数。这些参数可以用来解释自变量与因变量之间的关系，以及预测新的观测值的类别。

    有序逻辑回归在多个领域中都有应用，例如社会科学、医学研究、市场调研等。它可以帮助研究人员理解和预测有序分类变量的行为和影响因素，从而为决策提供有价值的信息。

    数据说明：

    背景说明：

有序逻辑回归是一种用于研究有序因变量与自变量之间关系的统计方法。它假设因变量服从一种有序分布，并利用最大似然估计方法来拟合模型。通过计算不同自变量水平下的对数几率比，该模型可以帮助我们理解自变量对因变量的影响。在这个研究中，我们使用有序逻辑回归来探究兄弟姐妹个数对某个因变量的影响，并通过模型结果进行解释和推断。

    分析结果如下所示：

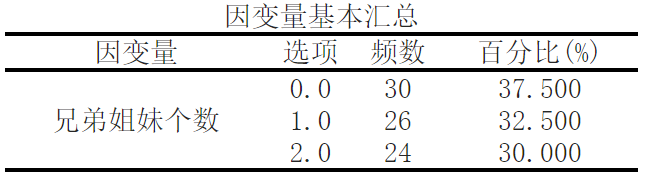
     将['A1', 'A2', 'A3']作为自变量，兄弟姐妹个数作为因变量进行二元Logit回归分析,从上表可以看出，总共有80个样本参加分析。

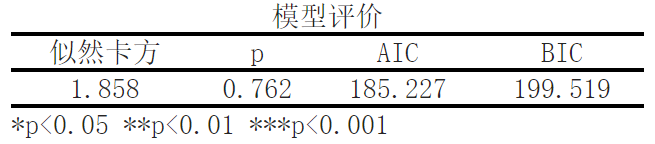
    模型的似然比卡方检验的结果显示，显著性P值0.762>0.05，水平上不呈现显著性，不能拒绝原假设，因而模型是无效的。

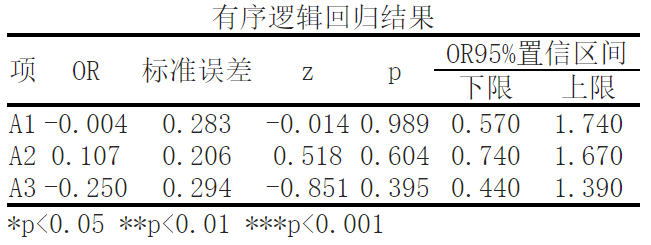
     基于变量A1，显著性P值为0.989，水平上不呈现显著性，不能拒绝原假设，因此A1不会对兄弟姐妹个数会产生显著性影响。

    基于变量A2，显著性P值为0.604，水平上不呈现显著性，不能拒绝原假设，因此A2不会对兄弟姐妹个数会产生显著性影响。

    基于变量A3，显著性P值为0.395，水平上不呈现显著性，不能拒绝原假设，因此A3不会对兄弟姐妹个数会产生显著性影响。

    在这个研究中，我们使用了有序逻辑回归模型来研究兄弟姐妹个数对某个因变量的影响。下面是对模型结果的解释：

    背景说明：

首先，让我们来看兄弟姐妹个数的基本汇总信息。在我们的样本中，有30个人没有兄弟姐妹（0.0），26个人有一个兄弟姐妹（1.0），24个人有两个兄弟姐妹（2.0）。

接下来，我们对模型进行了评价。似然卡方值为1.858，对应的p值为0.762，说明我们的模型的拟合效果尚可。AIC（赤池信息准则）值为185.227，BIC（贝叶斯信息准则）值为199.519，这两个指标用于评估模型的复杂度和拟合优度，数值越低表示模型越好。

最后，我们来看有序逻辑回归的结果。有序逻辑回归模型将自变量（这里是兄弟姐妹个数）与因变量之间的关系建模为一个有序分布。对于每个自变量，我们报告了其对数几率比（OR）和相应的统计指标。

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。