正态分布（Normal distribution）也叫常态分布，是连续随机变量概率分布的一种，其正态曲线的高峰位于正中央，即均数所在的位置。正态曲线以均数为中心，左右对称，曲线两端永远不与横轴相交。正态曲线由均数所在处开始，分别向左右两侧逐渐均匀下降。曲线与横轴间的面积总等于1，相当于概率密度函数的函数从正无穷到负无穷积分的概率为1。

    正态性检验用于检查数据是否服从正态分布。在统计学中，正态分布是一种常见的概率分布，具有对称的钟形曲线。了解数据是否符合正态分布对于确定适当的统计分析方法以及解释分析结果都至关重要。

    数据说明：

    背景说明：

    这些数据提供了不同样本（A1-A5）的平均值、标准差、偏度、峰度以及进行正态性检验所得的Kolmogorov-Smirnov检验p值和Shapiro-Wilk检验p值。这些数据可能来自于对某个特定变量进行的测量或观察，在统计分析前进行正态性检验可以帮助了解数据的分布情况，并选择合适的统计方法进行进一步分析和解释。根据给定的p值，我们可以推测这些样本数据在统计意义上不符合正态分布。

    结果显示：

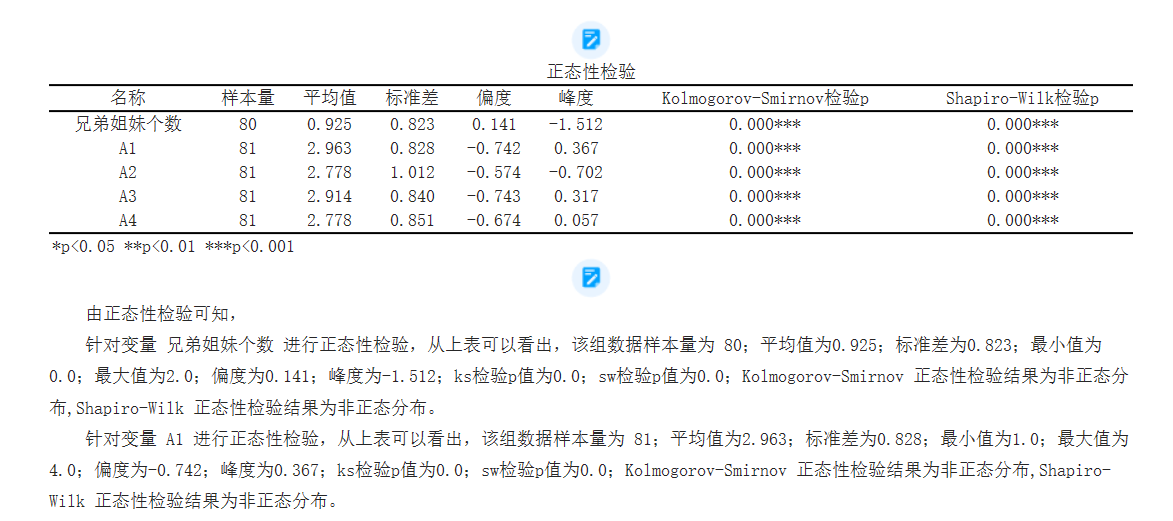
    由正态性检验可知，

    针对变量 A1 进行正态性检验，从上表可以看出，该组数据样本量为 81；平均值为2.963；标准差为0.828；最小值为1.0；最大值为4.0；偏度为-0.742；峰度为0.367；ks检验p值为0.0；sw检验p值为0.0；Kolmogorov-Smirnov 正态性检验结果为非正态分布,Shapiro-Wilk 正态性检验结果为非正态分布。

    针对变量 A2 进行正态性检验，从上表可以看出，该组数据样本量为 81；平均值为2.778；标准差为1.012；最小值为1.0；最大值为4.0；偏度为-0.574；峰度为-0.702；ks检验p值为0.0；sw检验p值为0.0；Kolmogorov-Smirnov 正态性检验结果为非正态分布,Shapiro-Wilk 正态性检验结果为非正态分布。

    针对变量 A3 进行正态性检验，从上表可以看出，该组数据样本量为 81；平均值为2.914；标准差为0.84；最小值为1.0；最大值为4.0；偏度为-0.743；峰度为0.317；ks检验p值为0.0；sw检验p值为0.0；Kolmogorov-Smirnov 正态性检验结果为非正态分布,Shapiro-Wilk 正态性检验结果为非正态分布。

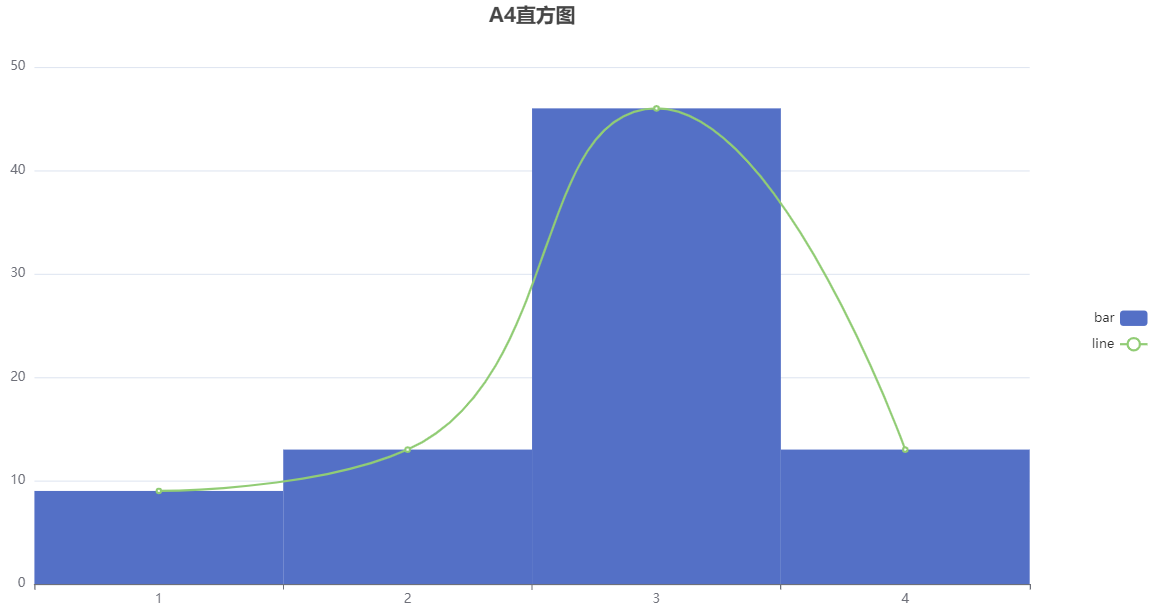
    针对变量 A4 进行正态性检验，从上表可以看出，该组数据样本量为 81；平均值为2.778；标准差为0.851；最小值为1.0；最大值为4.0；偏度为-0.674；峰度为0.057；ks检验p值为0.0；sw检验p值为0.0；Kolmogorov-Smirnov 正态性检验结果为非正态分布,Shapiro-Wilk 正态性检验结果为非正态分布。

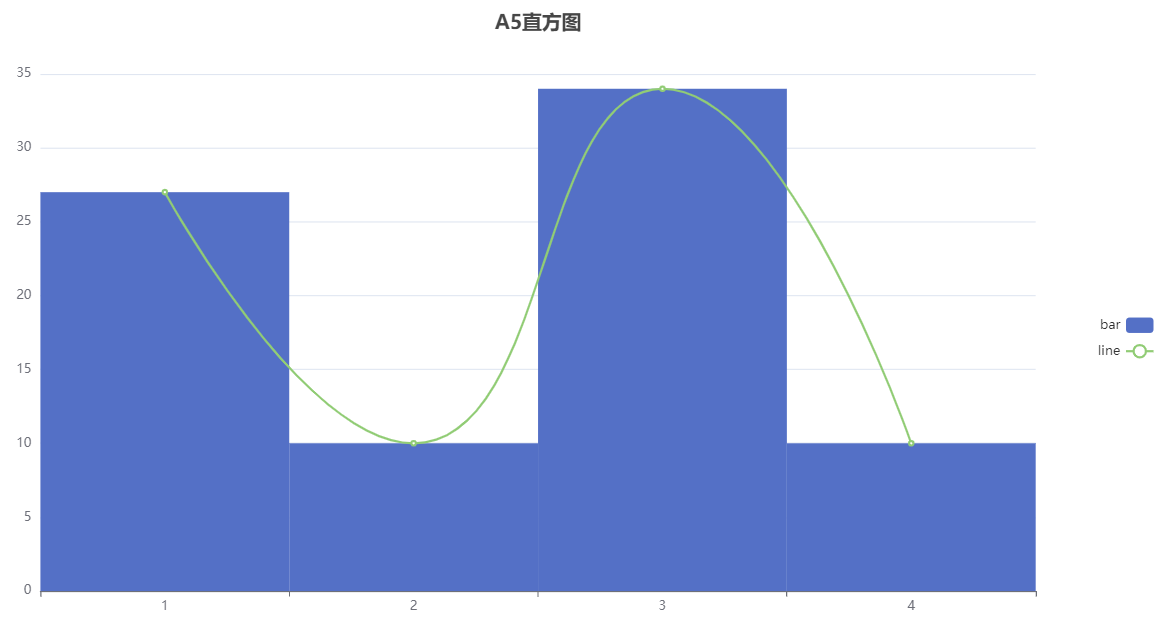
    针对变量 A5 进行正态性检验，从上表可以看出，该组数据样本量为 81；平均值为2.333；标准差为1.072；最小值为1.0；最大值为4.0；偏度为-0.083；峰度为-1.391；ks检验p值为0.0；sw检验p值为0.0；Kolmogorov-Smirnov 正态性检验结果为非正态分布,Shapiro-Wilk 正态性检验结果为非正态分布。

    结果指标解读：

    1. 样本量（Sample Size）：样本量是指数据集中的观察数量。较大的样本量可以提供更准确和可靠的统计结果。

    分析图形如下所示：

    2. 平均值（Mean）：平均值是一组数据的集中趋势的度量，表示数据的中心位置。

    3. 标准差（Standard Deviation）：标准差是一组数据的离散程度的度量，表示数据围绕平均值的分散程度。

    4. 偏度（Skewness）：偏度是数据分布的对称性度量。负偏度表示数据分布向左偏斜，正偏度表示数据分布向右偏斜。

    5. 峰度（Kurtosis）：峰度是数据分布曲线的陡峭程度的度量。正常分布的峰度为3，大于3表示峰度较高，小于3表示峰度较低。

    6. Kolmogorov-Smirnov检验p（Kolmogorov-Smirnov Test p-value）：Kolmogorov-Smirnov检验用于检验数据是否服从某个理论分布（如正态分布）。p值表示观察到的数据与理论分布之间差异的概率。

    7. Shapiro-Wilk检验p（Shapiro-Wilk Test p-value）：Shapiro-Wilk检验也用于检验数据是否服从正态分布。p值表示在零假设下，样本数据与正态分布一致的概率。

    分析图形如下所示：

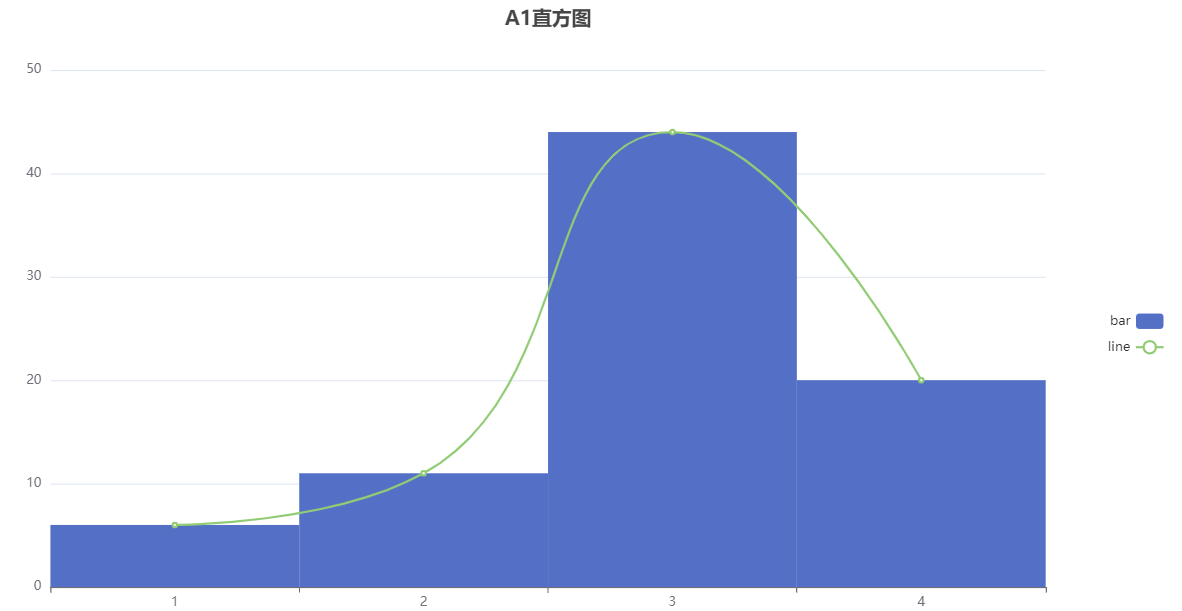
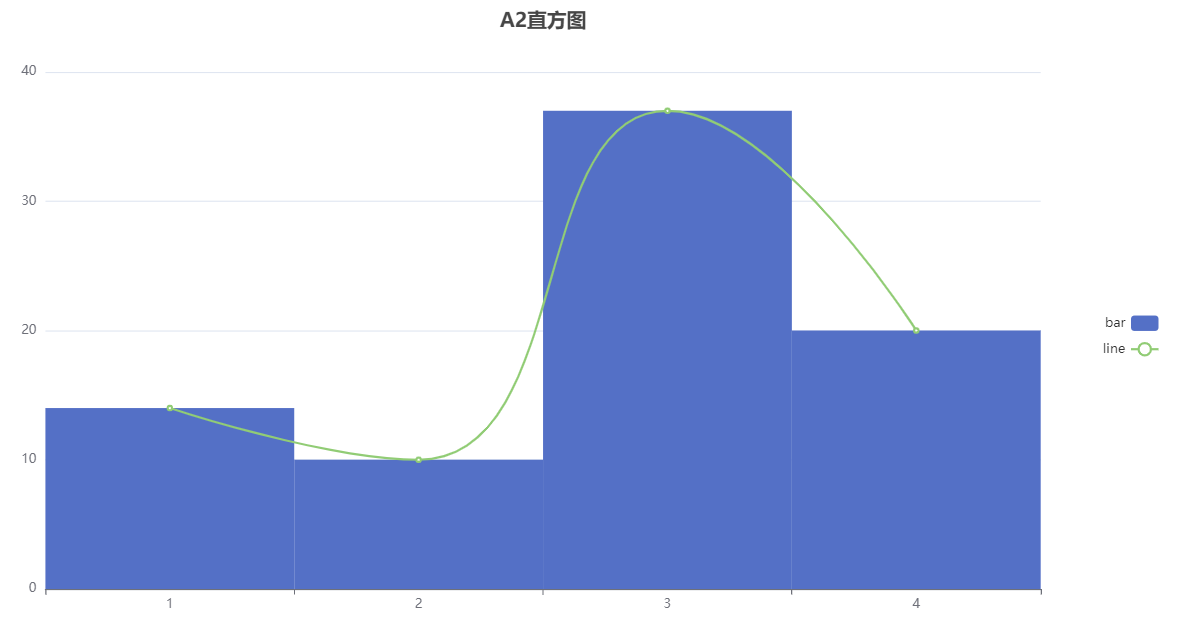
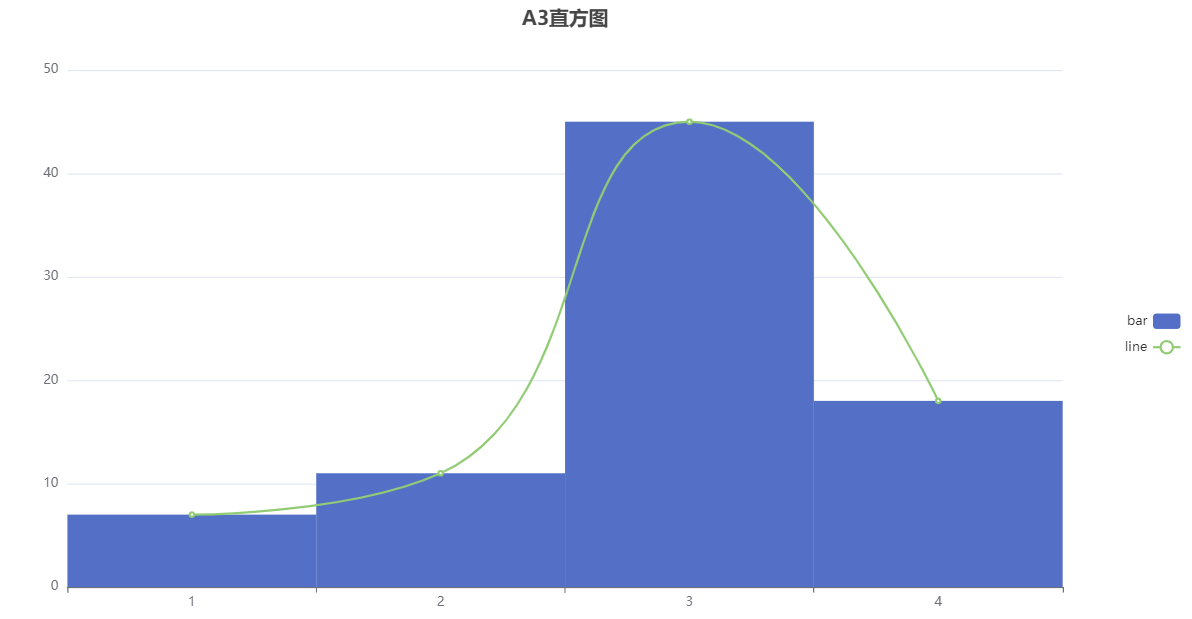
    [1]杨松林主编,文科数学,苏州大学出版社,2015.01,第107页

    [2]Shaou-Gang Miaou; Jin-Syan Chou. 《Fundamentals of probability and statistics》. 高立图书. 2012: 第147页.

    [3]胡泳. 正态分布[J]. 商务周刊, 2009 (24): 94-94.

    [4]Anderson T W, Anderson T W, Anderson T W, et al. An introduction to multivariate statistical analysis[M]. New York: Wiley, 1958.

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。