一种常用的多元线性回归模型选择和变量筛选方法。该方法的目的是通过逐步添加或删除自变量来找到最佳的回归模型，以使得得到的模型具有较好的预测能力和解释能力。在实际应用中，逐步回归方法是一种常用的变量筛选方法，能够通过逐步添加或删除自变量来找到最佳的回归模型。通过选择与因变量最相关的自变量，逐步回归方法可以提高模型的预测能力和解释能力。

    数据说明：

    背景说明：在这个研究中，我们关注了自变量A1到A9对因变量A10的影响。这些变量是通过1到5分的量表题获得的数据，用来评估参与者在某个特定问题上的态度或观点。为了分析这些变量之间的关系，我们使用了逐步回归方法。逐步回归是一种统计分析方法，通过逐步添加自变量来确定对因变量最具预测力的变量，从而构建最佳的回归模型。具体来说，逐步回归从常数项开始，逐步添加自变量，每次添加一个自变量，根据其对因变量的影响显著性来确定是否选择该变量。

    分析结果如下所示：

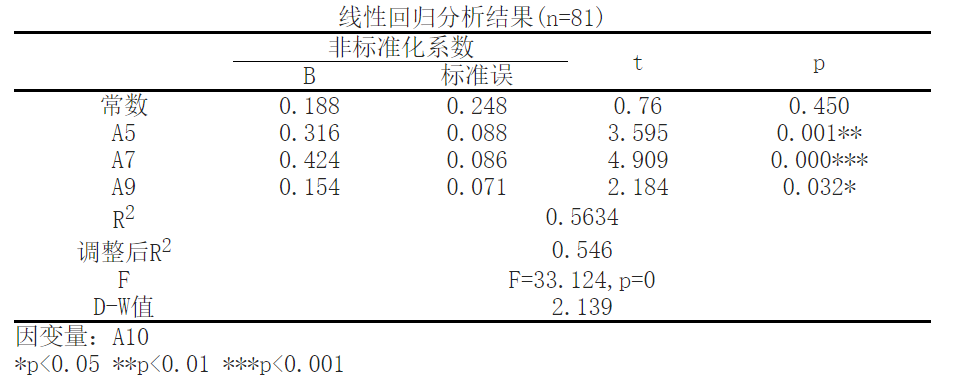
    由线性回归分析可知，结果显示，将A10作为因变量，['A5', 'A7', 'A9']作为自变量，建立自变量和因变量的多元回归模型，R2(RSquare) 代表回归模型中自变量对因变量变异的解释程度，是分析回归结果的开始，数据显示；模型R方值为0.5634,意味着['A5', 'A7', 'A9']可以解释A10的56.34%变化原因，通过F检验来判断回归模型的回归效果，即检验因变量与所有自变量之间的线性关系是否显著，也可以用来检验模型的统计学意义。由结果可得F值为33.124，P值为0.0，模型公式为：A10 = 0.188 + 0.316*A5 + 0.424*A7 + 0.154*A9。

    A5对A10存在显著正影响作用，beta值为0.3159，p值为0.0006(p<0.05)。

    A7对A10存在显著正影响作用，beta值为0.4238，p值为0.0(p<0.05)。

    A9对A10存在显著正影响作用，beta值为0.1541，p值为0.032(p<0.05)。

    参考文献：

    [1] Cohen, J., Cohen P., West, S.G., & Aiken, L.S. Applied multiple regression/correlation analysis for the behavioral sciences. Hillsdale, NJ: Lawrence Erlbaum Associates. 2003.

    [2] Draper, N.R. and Smith, H. Applied Regression Analysis. Wiley Series in Probability and Statistics. 1998.

    [3] 孙荣恒．应用数理统计（第三版）．北京：科学出版社，2014：204-206

    [4] alton, Francis. Regression Towards Mediocrity in Hereditary Stature (PDF). Journal of the Anthropological Institute. 1886, 15: 246–263

关注微信公众号发送【示例数据】获取SPSSMAX练习示例数据。